Mișcarea rectilinie și repausul sunt imposibile

Scris de **Abel Cavaşi** Mier 04 Aug 2021, 07:39

Rezumarea primului mesaj :

Iată o altă perspectivă asupra acestei chestiuni:

Curbura punctului este nedeterminată. Torsiunea dreptei este nedeterminată.

Dacă există un observator față de care curbura și torsiunea mișcării pot fi determinate, atunci acestea vor putea fi determinate pentru orice observator din Univers.

Astfel, mișcarea rectilinie și repausul sunt imposibile. Nu există vreun observator din Univers față de care un corp să se miște rectiliniu sau să fie în repaus.

Scris de **virgil** Lun 09 Aug 2021, 20:59

Abel Cavaşi a scris:
virgil a scris:Dar daca o metoda matematica nu poate indeparta nedeterminarea, prin metoda geometrica am gasit un raspuns valabil.
Metoda geometrică nu poate contrazice metoda matematică, căci geometria însăși este o ramură a matematicii.

In cazul dreptei obtinuta prin intersectia a doua plane perpendiculare, se poate atasa triedrul Frenet in orice punct al dreptei, in care normala este in planul orizontal iar binormala in planul vertical. Astfel triedrul Frenet poate glisa dealungul dreptei avand binormala mereu in aceiasi pozitie ceia ce inseamna torsiune zero.
Spune-mi ce nu este in ordine in acest caz?
Nu este în ordine definiția dreptei dată de tine. Dreapta nu este intersecția dintre două plane perpendiculare.

Matematica are mai multe discipline; aritmetica, analiza matematica, geometria plana, geometria in spatiu, geometria analitica, trigonometria, etc. Fiecare din aceste discipline demonstreaza adevarul matematic prin metode diferite dar care se completeaza una pe alta.
Privind figura triedrului Frenet aflat in miscare, vedem ca torsiunea este data de rotirea binormalei in jurul axei de deplasare. In cazul dreptei triedrul frenet se deplaseaza de-alungul dreptei, in timp ce binormala ramane mereu in acelasi plan.
https://ro.wiki2.wiki/wiki/Torsion_of_a_curve

Scris de **Abel Cavaşi** Lun 09 Aug 2021, 21:15

virgil a scris:
Abel Cavaşi a scris:
virgil a scris:Dar daca o metoda matematica nu poate indeparta nedeterminarea, prin metoda geometrica am gasit un raspuns valabil.
Metoda geometrică nu poate contrazice metoda matematică, căci geometria însăși este o ramură a matematicii.

In cazul dreptei obtinuta prin intersectia a doua plane perpendiculare, se poate atasa triedrul Frenet in orice punct al dreptei, in care normala este in planul orizontal iar binormala in planul vertical. Astfel triedrul Frenet poate glisa dealungul dreptei avand binormala mereu in aceiasi pozitie ceia ce inseamna torsiune zero.
Spune-mi ce nu este in ordine in acest caz?
Nu este în ordine definiția dreptei dată de tine. Dreapta nu este intersecția dintre două plane perpendiculare.
Matematica are mai multe discipline; aritmetica, analiza matematica, geometria plana, geometria in spatiu, geometria analitica, trigonometria, etc. Fiecare din aceste discipline demonstreaza adevarul matematic prin metode diferite dar care se completeaza una pe alta.
Privind figura triedrului Frenet aflat in miscare, vedem ca torsiunea este data de rotirea binormalei in jurul axei de deplasare. In cazul dreptei triedrul frenet se deplaseaza de-alungul dreptei, in timp ce binormala ramane mereu in acelasi plan.
https://ro.wiki2.wiki/wiki/Torsion_of_a_curve

Așa, și?

Scris de **virgil** Mar 10 Aug 2021, 07:00

Abel Cavaşi a scris:
virgil a scris:
Abel Cavaşi a scris:
Metoda geometrică nu poate contrazice metoda matematică, căci geometria însăși este o ramură a matematicii.

Nu este în ordine definiția dreptei dată de tine. Dreapta nu este intersecția dintre două plane perpendiculare.

Privind figura triedrului Frenet aflat in miscare, vedem ca torsiunea este data de rotirea binormalei in jurul axei de deplasare. In cazul dreptei triedrul frenet se deplaseaza de-alungul dreptei, in timp ce binormala ramane mereu in acelasi plan.
https://ro.wiki2.wiki/wiki/Torsion_of_a_curve
Așa, și?

Si nu ai dreptate. Prin metoda geometrica am ridicat nedeterminarea torsiunii pentru linia dreapta.

Scris de **Abel Cavaşi** Mar 10 Aug 2021, 14:14

virgil a scris:Privind figura triedrului Frenet aflat in miscare, vedem ca torsiunea este data de rotirea binormalei in jurul axei de deplasare. In cazul dreptei triedrul frenet se deplaseaza de-alungul dreptei, in timp ce binormala ramane mereu in acelasi plan.
https://ro.wiki2.wiki/wiki/Torsion_of_a_curve

Si nu ai dreptate. Prin metoda geometrica am ridicat nedeterminarea torsiunii pentru linia dreapta.

Puiule, nu te grăbi să tragi concluzii pripite. Ziceai, și bine ziceai, că binormala rămâne mereu ÎNTR-UN PLAN. Știi ce înseamnă asta? Că DOAR PLANUL poate fi determinat, puiule, nu și POZIȚIA binormalei în acel plan.

Scris de **eugen** Mar 10 Aug 2021, 14:26

Intr-un Univers real cu dinamica continua, in care se pot admite interactiuni la orice distanta, miscarea uniforma absoluta si repausul absolut pot fi doar imaginare...
Referentialul rectiliniu si punctul fix sunt sunt si ele imaginare...
Sa nu confundam realul cu conventionalul.

Scris de **virgil** Mar 10 Aug 2021, 17:24

Abel Cavaşi a scris:
virgil a scris:Privind figura triedrului Frenet aflat in miscare, vedem ca torsiunea este data de rotirea binormalei in jurul axei de deplasare. In cazul dreptei triedrul frenet se deplaseaza de-alungul dreptei, in timp ce binormala ramane mereu in acelasi plan.
https://ro.wiki2.wiki/wiki/Torsion_of_a_curve
Si nu ai dreptate. Prin metoda geometrica am ridicat nedeterminarea torsiunii pentru linia dreapta.
Puiule, nu te grăbi să tragi concluzii pripite. Ziceai, și bine ziceai, că binormala rămâne mereu ÎNTR-UN PLAN. Știi ce înseamnă asta? Că DOAR PLANUL poate fi determinat, puiule, nu și POZIȚIA binormalei în acel plan.

Prin conditiile initiale am impus cele doua plane perpendiculare, astfel incat in planul orizontal de exemplu se regaseste raza de curbura care in acest caz este infinita, iar in planul vertical se regaseste binormala care impreuna cu ditectia dreptei sa formeze triedrul Frenet. Glisand punctul de aplicatie a celor trei vectori dealungul dreptei, binormala va apartine in permanenta de planul vertical. Daca binormala nu se roteste in jurul dreptei inseamna ca torsiunea este zero.

Scris de **virgil** Mar 10 Aug 2021, 17:35

eugen a scris:Intr-un Univers real cu dinamica continua, in care se pot admite interactiuni la orice distanta, miscarea uniforma absoluta si repausul absolut pot fi doar imaginare...
Referentialul rectiliniu si punctul fix sunt sunt si ele imaginare...
Sa nu confundam realul cu conventionalul.

Referitor la repausul absolut am imaginat o metoda teoretica de determinare a unui punct fix in spatiu;
"Virgil;
Teoretic vorbind cred ca s-ar putea stabili un punct de repaus absolut din spatiu folosind trei surse laser legate de o nava plasate pe trei tentacule rectangulare a caror raze sa se intalneasca intr-un punct. Nava este in miscare pe o traiectorie oarecare si la un moment dat emite un impuls simultan. Stim ca in acelasi sistem de referinta viteza luminii este o constanta, dar mai stim ca traiectoria razei laser este rectilinie si nu este influientata de traiectoria sursei. Deci razele odata emise simultan se vor intalni intr-un punct care este fix in univers observat de nava in miscarea ei ca fiind vizibil datorita interferentei constructive. Un observator computerizat va putea folosi acel punct de reper pentru a determina traiectoria absoluta a navei in univers. Desigur sunt necesare o succesiune de astfel de puncte de reper astfel incat observatorul din nava sa poata determina traiectoria."

Scris de **Abel Cavaşi** Mar 10 Aug 2021, 18:52

virgil a scris:Daca binormala nu se roteste in jurul dreptei inseamna ca torsiunea este zero.

Dacă! Dar cine știe în ce poziție este? Pe ce criterii îi stabilești poziția? Oriunde ar fi ea în planul normal, dreapta tot dreaptă rămâne. Deci, torsiunea dreptei rămâne nedeterminată.

Scris de **virgil** Mar 10 Aug 2021, 19:12

Abel Cavaşi a scris:
virgil a scris:Daca binormala nu se roteste in jurul dreptei inseamna ca torsiunea este zero.
Dacă! Dar cine știe în ce poziție este? Pe ce criterii îi stabilești poziția? Oriunde ar fi ea în planul normal, dreapta tot dreaptă rămâne. Deci, torsiunea dreptei rămâne nedeterminată.

Evident ca triedrul Frenet atasat unui punct apartinand dreptei poate avea orice orientare in jurul punctului, dar de la bun inceput aleg ca normala si binormala sa apartina celor doua planuri perpendiculare. Aceste planuri la randul lor pot ocupa orice pozitie in jurul dreptei, dar de fiecare data va contine triedrul Frenet pentru ca asa mi-am propus. Glisarea punctului de aplicatie dea-lungul dreptei va face ca binormala sa fie continuta totdeauna in planul ales. Deci torsiunea de fiecare data va fi zero.

Scris de **Abel Cavaşi** Mar 10 Aug 2021, 19:15

Deci insiști în continuare. Nu vrei să înțelegi că varianta aleasă de tine NU ESTE GENERALĂ. Este un caz particular. Nimic nu-ți dă dreptul să particularizezi. Nimic nu-ți dă dreptul să consideri că binormala unei drepte este în repaus într-o poziție determinată.

Scris de **Razvan** Mar 10 Aug 2021, 19:57

Abel, nu ştiu dacă te-ai gândit, dar teoria ta ar putea fi similară cu Relativitatea Generală Einstein - Cartan, dacă o aplici la geodezicele spaţiu-timpului. Ai încercat să vezi ce iese? Poate ar rezulta o exprimare matematică mai facilă decât cea din TRG. Zic şi eu, e doar o idee..
https://arxiv.org/abs/gr-qc/0606062

Scris de **virgil** Mar 10 Aug 2021, 20:07

Abel Cavaşi a scris:Deci insiști în continuare. Nu vrei să înțelegi că varianta aleasă de tine NU ESTE GENERALĂ. Este un caz particular. Nimic nu-ți dă dreptul să particularizezi. Nimic nu-ți dă dreptul să consideri că binormala unei drepte este în repaus într-o poziție determinată.

Cred ca nu intelegi prea bine ce inseamna torsiunea. Daca verific intr-o suta de puncte si o suta de pozitii ale celor doua plane si totdeauna binormala se afla in plan, torsiunea este zero. De fapt torsiunea nu se afla in dreapta respectiva pentru ca aceasta are sectiunea zero, torsiunea este o consecinta corpului care urmeaza traiectoria respectiva, si caruia poti sa-i atasezi un triedru Frenet in centrul de masa. Am aratat in al doilea exemplu ca doua suprafete elicoidale se pot intersecta dupa o dreapta, dar de data aceasta dreapta va avea torsiunea diferita de zero. Cum este posibil ca aceiasi dreapta sa aiba odata torsiunea zero si in al doilea caz sa aiba torsiunea diferita de zero? Este posibil pentru ca traiectoria poarta informatia miscarii corpului in spatiu, si fara corp nu exista traiectoria.

Scris de **Abel Cavaşi** Mar 10 Aug 2021, 20:24

virgil a scris:Cred ca nu intelegi prea bine ce inseamna torsiunea.

Desigur. Asta era.

Scris de **Abel Cavaşi** Mar 10 Aug 2021, 20:24

Razvan a scris:Abel, nu ştiu dacă te-ai gândit, dar teoria ta ar putea fi similară cu Relativitatea Generală Einstein - Cartan, dacă o aplici la geodezicele spaţiu-timpului. Ai încercat să vezi ce iese? Poate ar rezulta o exprimare matematică mai facilă decât cea din TRG. Zic şi eu, e doar o idee..
https://arxiv.org/abs/gr-qc/0606062

Nicio teorie prezentă nu are echivalent cu ceea ce propun eu. Dacă ar fi avut, atunci ar fi schimbat principiul inerției.

Scris de **eugen** Mier 11 Aug 2021, 12:07

O consecinta care ar rezulta in virtutea enuntului -titlu al topicului ar fi ca toate interpretarile energiei mecanice calculate cu trasee rectilinii ar trebui reevaluate.
Adica o entitate are nu numai energie in translatie ci si in rotatie.
Daca rotatia este subestimata, energia in rotatie este subestimata.
Observatorul "orb" la rotatii ( specifice microcosmosului ) risca erori.
Un exemplu de matematician care a inteles aceste subtilitati a fost Maxwell.
Probabil este premergatorul unificarii fortelor electrice, magnetice si mecanice prin eterul elicoidal.

Scris de **virgil_48** Mier 11 Aug 2021, 12:13

Abel Cavaşi a scris:
Razvan a scris:Abel, nu ştiu dacă te-ai gândit, dar teoria ta ar putea fi similară cu Relativitatea Generală Einstein - Cartan, dacă o aplici la geodezicele spaţiu-timpului. Ai încercat să vezi ce iese? Poate ar rezulta o exprimare matematică mai facilă decât cea din TRG. Zic şi eu, e doar o idee..
https://arxiv.org/abs/gr-qc/0606062
Nicio teorie prezentă nu are echivalent cu ceea ce propun eu. Dacă ar fi avut, atunci ar fi schimbat principiul inerției.

Te referi la teoriile recunoscute. Dar tu ai auzit si de teoria lui
WoodyCAD.
Nu exista apropieri ?

Scris de **Abel Cavaşi** Mier 11 Aug 2021, 12:32

virgil_48 a scris:Dar tu ai auzit si de teoria lui
WoodyCAD.
Nu exista apropieri ?

Există apropieri. „Teoria” lui este inginerească, emanată de un inginer, deci fără definiții teoretice solide, motiv pentru care nu poate face raționamente generale, ci speculează niște legi experimentale. Marea valoare a „teoriei” sale este că scoate în evidență rolul elicei. Dar, desigur, este DEPARTE de principiul elicoidal a inerției.

Scris de **virgil_48** Mier 11 Aug 2021, 15:28

Abel Cavaşi a scris:
virgil_48 a scris:Dar tu ai auzit si de teoria lui
WoodyCAD.
Nu exista apropieri ?
Există apropieri. „Teoria” lui este inginerească, emanată de un inginer, deci fără definiții teoretice solide, motiv pentru care nu poate face raționamente generale, ci speculează niște legi experimentale. Marea valoare a „teoriei” sale este că scoate în evidență rolul elicei. Dar, desigur, este DEPARTE de principiul elicoidal a inerției.

Am inteles din citat. WoodyCAD nu a demonstrat ca miscarea
rectilinie este imposibila ca un inginer, iar tu ca un teoretician.
Ar trebui sa primiti amandoi multumiri din partea lui Newton
pentru aceasta incercare.

Scris de **virgil** Mier 11 Aug 2021, 19:08

eugen a scris:O consecinta care ar rezulta in virtutea enuntului -titlu al topicului ar fi ca toate interpretarile energiei mecanice calculate cu trasee rectilinii ar trebui reevaluate.
Adica o entitate are nu numai energie in translatie ci si in rotatie.
Daca rotatia este subestimata, energia in rotatie este subestimata.
Observatorul "orb" la rotatii ( specifice microcosmosului ) risca erori.
Un exemplu de matematician care a inteles aceste subtilitati a fost Maxwell.
Probabil este premergatorul unificarii fortelor electrice, magnetice si mecanice prin eterul elicoidal.

Din studiul meu asupra planetelor sistemului solar rezulta ca exista o corelatie intre miscarea de rotatie in jurul axei proprii si miscarea de orbitare in jurul Soarelui. Chiar am stabilit o relatie intre cele doua miscari.
Cititi aici incepand cu pag.88-92.

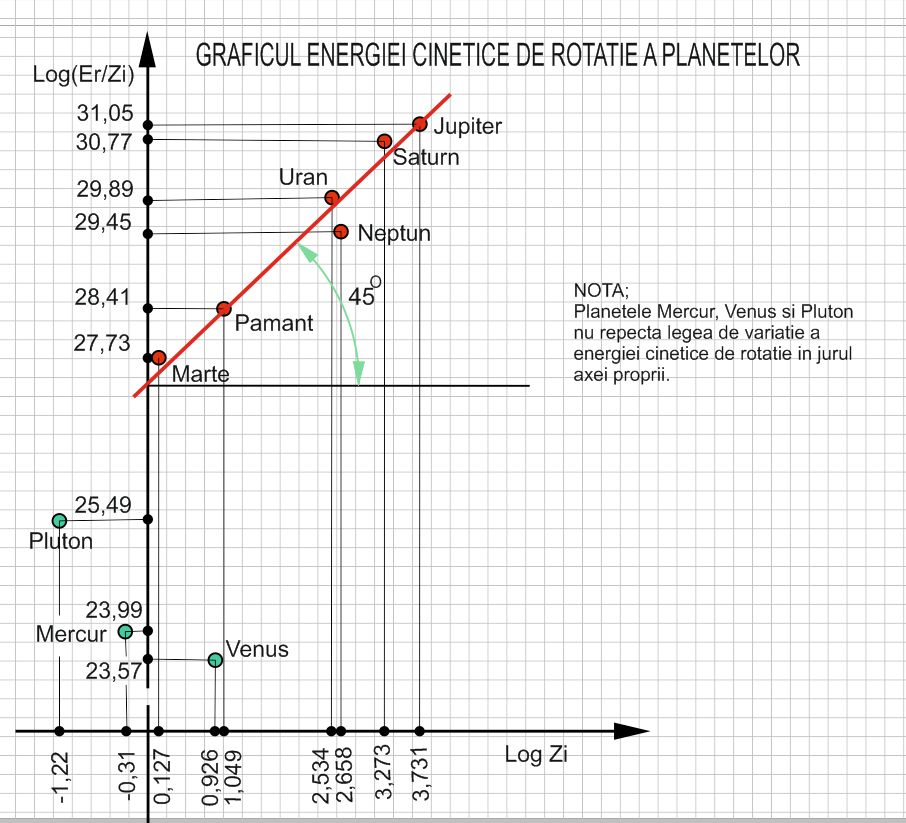
Mișcarea rectilinie și repausul sunt imposibile - Pagina 3 Grafic27

https://drive.google.com/file/d/1dKTnctVAdSsbGliwZMFJ2ynbIMwVIEk7/view?usp=sharing

Scris de **gafiteanu** Joi 12 Aug 2021, 19:18

Baieti, vad ca e imposibil sa va opriti, sa luati si voi un repaus. Doar in repaus se poate gandi corect, in liniste. Si multe alte chestii se pot face doar in repaus. Asa dar, exista repaus...
Cica la Radio Erevan se pune urmatoarea intrebare: -Pot face dragoste in fuga alergand un barbat si o femeie ? Si vine raspunsul: -Nu, deoarece o femeie cu fustele in cap alearga mult mai repede decat un barbat cu pantalonii in vine... Asa ca doar in repaus am fost cu totii procreati, cum spun si versurile lui Eminescu:
https://replici.net/replici-din-teatru-radiofonic/replici-si-citate-audio-din-poezii-de-mihai-eminescu/din-chaos-doamne-am-aparut-si-m-as-intoarce-n-chaos-si-din-repaos-m-am-nascut-mi-e-sete-de-repaos

Scris de **virgil_48** Sam 14 Aug 2021, 16:28

eugen a scris:. . . . .
Adica o entitate are nu numai energie in translatie ci si in rotatie.
Daca rotatia este subestimata, energia in rotatie este subestimata.
Observatorul "orb" la rotatii ( specifice microcosmosului ) risca erori.
Un exemplu de matematician care a inteles aceste subtilitati a fost Maxwell.
Probabil este premergatorul unificarii fortelor electrice, magnetice si mecanice prin eterul elicoidal.

Alunecarea in microcosmos si electrotehnica, nu poate modifica
principiile mecanicii, cele mai verificate, logice si usor de inteles.
Bineinteles ca o entitate poate avea energie de translatie si de
rotatie. Daca are. Adica aceea care i-a fost imprimata initial,
poate fi si numai una singura dintre cele doua sau niciuna.
Miscarea de rotatie nu este obligatorie, ca de fapt nici cea de
translatie si in nici un caz nu sunt implicite.
Considerarea miscarii de rotatie ca o anexa permanenta a
miscarii de translatie este numai o ambitie personala a unora.
In plus, miscarea de rotatie care poate insoti miscarea de
translatie a unui singur corp, este numai cea in jurul centrului
sau de greutate.
Asta este mecanica elementara, nu este ca asa vreau eu. Daca
nu recunosti mecanica, nu vorbesti despre de miscarea corpurilor.
Despre miscarea din microcosmos se pot spune multe, fiindca
este greu sau imposibil de verificat. Si atunci infloreste fantezia.

Scris de **virgil** Sam 14 Aug 2021, 16:47

Nimic nu este intamplator; cum se face ca nici un satelit natural nu are miscare de rotatie in jurul axei proprii, in timp ce planetele si stelele au aceasta miscare de rotatie ?

Scris de **Abel Cavaşi** Sam 14 Aug 2021, 17:31

virgil_48 a scris:Considerarea miscarii de rotatie ca o anexa permanenta a
miscarii de translatie este numai o ambitie personala a unora.

Iar începi cu atacul la persoană? Nu-ți dai seama că n-ai demonstrat nimic, încât să ai dreptul să susții asemenea tâmpenii?

Asta este mecanica elementara, nu este ca asa vreau eu.

Tu nu cunoști nici măcar această „mecanică elementară”.

Daca
nu recunosti mecanica, nu vorbesti despre de miscarea corpurilor.
Despre miscarea din microcosmos se pot spune multe, fiindca
este greu sau imposibil de verificat. Si atunci infloreste fantezia.

Se pare că ai uitat, din nou, definiția „fanteziei” cu care te-ai lăudat deunăzi că nu ataci persoana.

Scris de **virgil_48** Sam 14 Aug 2021, 19:28

Abel Cavaşi a scris:
virgil_48 a scris:Considerarea miscarii de rotatie ca o anexa permanenta a
miscarii de translatie este numai o ambitie personala a unora.
Iar începi cu atacul la persoană? Nu-ți dai seama că n-ai demonstrat nimic, încât să ai dreptul să susții asemenea tâmpenii?

Ce pot sa-ti fac daca tu tot timpul iti pui o țintă pe piept?
Ai impresia ca fantezia elicoidala ai inventat-o tu? Ceace am
scris in raspunsul acela este mecanica elementara. Nu are
nevoie de demonstratie, poti citi niste manuale.
Daca nu mai poti sa suporti mecanica actuala, dece nu cauti
sa autentifici alta? Toti cei care vin cu idei "revolutionare", nu
pot pretinde sa li se demonstreze din nou cele vechi. Trebuie
sa demonstreze ei ca parerile lor sunt cele adevarate.
Si mai ai in vedere diferenta dintre o fantezie si o tampenie.
Nu poti de loc sa te controlezi.

Scris de **Abel Cavaşi** Sam 14 Aug 2021, 19:31

Și mai ai și tupeu...

Scris de **virgil_48** Sam 14 Aug 2021, 19:49

Abel Cavaşi a scris:Și mai ai și tupeu...

Poti sa mai evaluezi si diferenta dintre "tupeu" si "lipsa de
control" !

Scris de **Abel Cavaşi** Sam 14 Aug 2021, 19:50

Și neobrăzare...

Scris de **Abel Cavaşi** Vin 17 Dec 2021, 09:36

Pentru cei care încă nici acum nu au înțeles problematica repausului și a mișcării rectilinii, am mai scris un material, sper că mai clar:
https://docs.google.com/document/d/1OMvXV0lAfiAjDpa7oEtJYNWemnqEjy5TU1aPonS8HlE/edit?usp=sharing

Scris de **virgil** Vin 17 Dec 2021, 10:40

Abel Cavaşi a scris:Pentru cei care încă nici acum nu au înțeles problematica repausului și a mișcării rectilinii, am mai scris un material, sper că mai clar:
https://docs.google.com/document/d/1OMvXV0lAfiAjDpa7oEtJYNWemnqEjy5TU1aPonS8HlE/edit?usp=sharing

Frumos referatul tau, dar cred ca are o hiba si anume, proprietatile rapoartelor a doua numere nu poate fi comparate cu proprietatile rapoartelor a doua functii.

Scris de **Abel Cavaşi** Vin 17 Dec 2021, 13:58

virgil a scris:proprietatile rapoartelor a doua numere nu poate fi comparate cu proprietatile rapoartelor a doua functii.

Îmi dai ceva detalii? Sau te mulțumești cu acest mesaj?

Scris de **virgil** Vin 17 Dec 2021, 17:02

Abel Cavaşi a scris:
virgil a scris:proprietatile rapoartelor a doua numere nu poate fi comparate cu proprietatile rapoartelor a doua functii.
Îmi dai ceva detalii? Sau te mulțumești cu acest mesaj?

Dupa cum se vede curbura si torsiunea sunt exprimate prin derivatele simple si duble a unor functiii care apoi se raporteaza intre ele. Dar daca derivezi niste numere si vei obine totdeauna zero, iar raportul lor totdeauna va da o nedeterminare 0/0 ; Deci nu cred ca poti extinde proprietatile numerelor la functii. Cred ca ar trebui luate niste exemple concrete si pentru functii asa cum ai facut pentru numere.

Scris de **virgil_48** Vin 17 Dec 2021, 17:25

Crezi ca poti sustine o ipoteza atat de radicala cu argumente
din nedeterminari ?!
Cu acelea poti dovedi orice, doar stii cum se face !

Scris de Continut sponsorizat

Mișcarea rectilinie și repausul sunt imposibile

Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile

Re: Mișcarea rectilinie și repausul sunt imposibile