Ultimele subiecte
» Impulsul elicoidalScris de virgil Joi 25 Iul 2024, 17:43
» New topic
Scris de virgil Mier 24 Iul 2024, 07:33
» Ce fel de popor suntem
Scris de CAdi Mar 23 Iul 2024, 22:12
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Mar 23 Iul 2024, 06:47
» Fenomene Electromagnetice
Scris de eugen Lun 22 Iul 2024, 21:37
» Sa mai auzim si de bine in Romania :
Scris de virgil Lun 22 Iul 2024, 18:39
» Masina Timpului
Scris de CAdi Lun 22 Iul 2024, 13:17
» Globalizarea
Scris de virgil Dum 21 Iul 2024, 16:46
» Unde a ajuns stiinta ?
Scris de CAdi Dum 21 Iul 2024, 15:20
» Ce este FOIP?
Scris de Abel Cavaşi Vin 19 Iul 2024, 22:02
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de CAdi Joi 18 Iul 2024, 11:51
» Inertia
Scris de virgil Mier 17 Iul 2024, 11:09
» Lucrul mecanic - definitie si exemple (Secţiunea 2)
Scris de CAdi Mar 16 Iul 2024, 05:20
» Laborator-sa construim impreuna
Scris de eugen Lun 15 Iul 2024, 10:17
» Stanley A. Meyer - Hidrogen
Scris de eugen Dum 14 Iul 2024, 20:25
» Despre vise
Scris de CAdi Sam 13 Iul 2024, 15:09
» Constatari
Scris de curiosul Sam 13 Iul 2024, 10:13
» Pendulul
Scris de virgil_48 Lun 08 Iul 2024, 16:18
» Marea teorema a lui Fermat.
Scris de curiosul Sam 06 Iul 2024, 10:23
» Legi de conservare (2)
Scris de Vizitator Vin 05 Iul 2024, 13:24
» PROFILUL CERCETATORULUI...
Scris de virgil Dum 30 Iun 2024, 19:01
» Grup de cercetare pentru constiinta
Scris de curiosul Sam 29 Iun 2024, 16:06
» CURIOZITATI; Motor miniatural functional
Scris de virgil Vin 28 Iun 2024, 20:36
» Fizicieni care au schimbat lumea.
Scris de eugen Vin 28 Iun 2024, 09:58
» O proprietate Black Hole (Gaura Neagra)
Scris de virgil Joi 27 Iun 2024, 17:58
» Cum marim energia atomului ?
Scris de virgil Dum 23 Iun 2024, 19:11
» Bec Tapo L530E 2.0 - Smart Wi-Fi Light Bulb, Multicolor
Scris de Dacu Vin 21 Iun 2024, 18:30
» Caracteristicile tehnice ale motoarelor auto
Scris de CAdi Joi 20 Iun 2024, 12:24
» Concluzii asupra relativității
Scris de curiosul Dum 16 Iun 2024, 11:55
» EMINESCU, Templu National
Scris de eugen Sam 15 Iun 2024, 22:29
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT... ( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la virgil în Sa mai auzim si de bine in Romania :
( 2 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 2 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12347) | ||||
| CAdi (12205) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7950) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6162) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3889) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 11 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 11 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Simetrie binomială
4 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Simetrie binomială
Simetrie binomială
Oare asta să fi fost demonstrația lui Fermat?
Se spune că într-o scrisoare trimisă lui Euler, parcă, Fermat menționa că are o demonstrație pentru presupunerea lui, că x^n+y^n=z^n nu are soluții naturale x, y, z pentru n>2, dar nu i-ar ajunge marginea paginii.
Sau ceva de genul.
Se pare că s-ar putea demonstra folosind o matematică elementară, dar bazată pe o anumită proprietate de "simetrie binomială", pe care eu personal nu am mai văzut-o nicăieri menționată.
Și destul de ușor de verificat pentru oricine cunoaște un nivel de matematică de liceu.
Caracterul nou este această "simetrie binomială" care, adaptate la soluțiile ecuației, duce la anumite concluzii în ce privește primitivitatea soluțiilor ecuației.
Voi expune în continuare acest aspect și pentru că scriu de pe mobil voi prefera să expun, tot la fel, sub formă de imagini, metoda de inserare a ecuațiilor în LaTex pe forum fiind destul de costisitoare de pe mobil.
Se spune că într-o scrisoare trimisă lui Euler, parcă, Fermat menționa că are o demonstrație pentru presupunerea lui, că x^n+y^n=z^n nu are soluții naturale x, y, z pentru n>2, dar nu i-ar ajunge marginea paginii.
Sau ceva de genul.
Se pare că s-ar putea demonstra folosind o matematică elementară, dar bazată pe o anumită proprietate de "simetrie binomială", pe care eu personal nu am mai văzut-o nicăieri menționată.
Și destul de ușor de verificat pentru oricine cunoaște un nivel de matematică de liceu.
Caracterul nou este această "simetrie binomială" care, adaptate la soluțiile ecuației, duce la anumite concluzii în ce privește primitivitatea soluțiilor ecuației.
Voi expune în continuare acest aspect și pentru că scriu de pe mobil voi prefera să expun, tot la fel, sub formă de imagini, metoda de inserare a ecuațiilor în LaTex pe forum fiind destul de costisitoare de pe mobil.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Pentru n>2.
Dar e o greșeală pe ultima pagină.
În fiecare serie trebuie adăugat în termenii din stânga z, z^2, z^3,....
Nu schimbă mare lucru în concluzie.
Cred.
Analiza a fost făcută în timp ce lucram la serviciu și am fost foarte entuziasmat sa o descriu, fără să stau să o analizez profund.
Am scris-o așa cum am gandit-o.
Dar e o greșeală pe ultima pagină.
În fiecare serie trebuie adăugat în termenii din stânga z, z^2, z^3,....
Nu schimbă mare lucru în concluzie.
Cred.
Analiza a fost făcută în timp ce lucram la serviciu și am fost foarte entuziasmat sa o descriu, fără să stau să o analizez profund.
Am scris-o așa cum am gandit-o.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Și mai este o greșeală pe pagina 2.
Inițial am considerat că a=b+c deși am dezvoltat ca și cum a=c.
Dar cine vrea să înțeleagă, înțelege greșeala și..o pardonează.
Inițial am considerat că a=b+c deși am dezvoltat ca și cum a=c.
Dar cine vrea să înțeleagă, înțelege greșeala și..o pardonează.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Dacă nu ma pripesc în afirmații, ar fi o o analiza care se conformează unei "forme modulare' prin care s-a și demonstrat teorema.
Dar apelând la alte structuri matematice, deși "adevărul" era la picioarele noastre. Poate. Cumva.
Ceea ce ma face ce să cred că nu întotdeauna ceea ce nu poate fi demonstrat necesită alte perspective pentru a fi demonstrat.
Dacă, să presupunem, ceea ce am prezentat ar fi corect, ar fi un foarte bun motiv să înțelegem că ceea ce se consideră imposibil este posibil din perspectiva unuia care nu știe ce este posibil și ce nu este posibil.
Dar apelând la alte structuri matematice, deși "adevărul" era la picioarele noastre. Poate. Cumva.
Ceea ce ma face ce să cred că nu întotdeauna ceea ce nu poate fi demonstrat necesită alte perspective pentru a fi demonstrat.
Dacă, să presupunem, ceea ce am prezentat ar fi corect, ar fi un foarte bun motiv să înțelegem că ceea ce se consideră imposibil este posibil din perspectiva unuia care nu știe ce este posibil și ce nu este posibil.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Așa cum voi ați spune "la locul potrivit în momentul potrivit" eu aș spune "omul potrivit pentru problema potrivită".
Eu am multe probleme, să vedem dacă sunt potrivit pentru toate.
Iar eu am în principal o problemă cu numerele prime.
Eu am multe probleme, să vedem dacă sunt potrivit pentru toate.
Iar eu am în principal o problemă cu numerele prime.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
O altă constatare la același nivel de "simetrie binomială" este următorul aspect.
Putem scrie z^n-x^n sub formă de 2 factori și anume:

Pentru n impar și doar pentru n impar, al doilea factor (paranteza mai lungă) poate fi scris într-o formă foarte interesantă folosind toți factorii "binomiali" (combinații de n luate câte x) în felul următor:

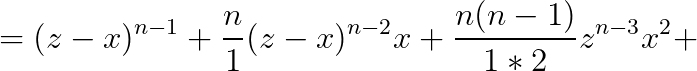

Cu alte cuvinte, dacă în loc de z schimbam cu z-x, amplificând toți ceilalți termeni în mod consecutiv cu exact factorii "binomiali" consecutivi se obține factorul lui z^n-x^n.
Dar asta doar pentru n impar.
Pentru n par nu funcționează.
Putem scrie z^n-x^n sub formă de 2 factori și anume:

Pentru n impar și doar pentru n impar, al doilea factor (paranteza mai lungă) poate fi scris într-o formă foarte interesantă folosind toți factorii "binomiali" (combinații de n luate câte x) în felul următor:

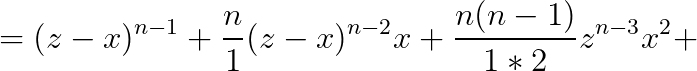

Cu alte cuvinte, dacă în loc de z schimbam cu z-x, amplificând toți ceilalți termeni în mod consecutiv cu exact factorii "binomiali" consecutivi se obține factorul lui z^n-x^n.
Dar asta doar pentru n impar.
Pentru n par nu funcționează.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Coreland acest aspect cu ceea ce este menționat anterior în subiect și scriind z-x = x+(z-2x), în egalitatea de mai sus, în partea dreapta în loc de x putem să scriem z-2x.
Edit:
De fapt, nu greșesc.
Revin.
Edit:
De fapt, nu greșesc.
Revin.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Cred că pot să arăt că este imposibilă relația de mai sus.
Adică este valabilă doar dacă z=3x.
Iar asta este valabilă doar pentru n impar.
Edit- mai sunt câteva greșeli pe ici, pe colo, dar doar de redactare.
Cred. Trebuie să verific.
Adică este valabilă doar dacă z=3x.
Iar asta este valabilă doar pentru n impar.
Edit- mai sunt câteva greșeli pe ici, pe colo, dar doar de redactare.
Cred. Trebuie să verific.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
E greșit.
Și de fapt, funcționează și pentru n par, am calculat eu greșit.
Și de fapt, funcționează și pentru n par, am calculat eu greșit.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Nu știu în ce măsură poate fi de folos acum, dar cu siguranță este un rezultat ce consider că merită menționat.
Se poate demonstra că în dezvoltarea lui z^n-x^n :
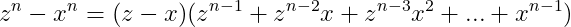
factorul din dreapta, paranteza mai lungă, poate fi scrisă sub forma următoare
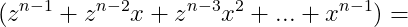
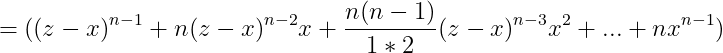
Adică cu excepția lui (z-x)^(n-1) toți ceilalți termeni conțin în mod consecutivi coeficienții binomiali din dezvoltarea binomului lui Newton pentru exponentul n.
În schimb, toți acești coeficienți ai tuturor termenilor îi putem scrie în mod consecutiv în felul următor:

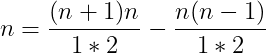
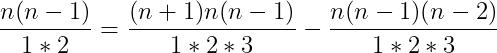
...
Continuând în aceeași manieră observăm că pot fi scriși coeficienții binomiali ai lui n în funcție de n+1.
Înlocuind în exprimarea factorului reprezentat de paranteza lungă din exprimarea lui z^n-x^n, putem să separăm exprimarea în funcție de coeficienții binomiali pentru exponentul n+1 și coeficienții binomiali pentru exponentul n.
Dezvoltând se ajunge generalizat la o exprimare de genul:
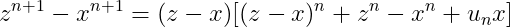
unde u_n este factorul reprezentat de "paranteza mare" din exprimarea lui z^n-x^n.
Exprimând z^(n+1)-x^(n+1) în aceeași manieră cum a fost exprimat z^n-x^n, simplificând cu (z-x) se ajunge la o exprimare identică doar cu exponentul crescut cu o unitate și indicele lui u crescut cu o unitate, aceasta putând fi considerată o relație de recurență generalizată.
Înlocuind tot timpul valorile lui u_n, u_(n-1), u_(n-2),... se ajunge la o exprimare interesantă.
Nu știu deocamdată la ce poate ajuta, dar am considerat că merită menționată în subiect.
Se poate demonstra că în dezvoltarea lui z^n-x^n :
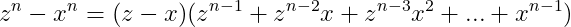
factorul din dreapta, paranteza mai lungă, poate fi scrisă sub forma următoare
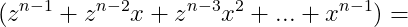
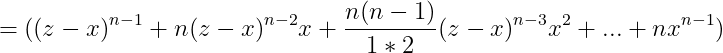
Adică cu excepția lui (z-x)^(n-1) toți ceilalți termeni conțin în mod consecutivi coeficienții binomiali din dezvoltarea binomului lui Newton pentru exponentul n.
În schimb, toți acești coeficienți ai tuturor termenilor îi putem scrie în mod consecutiv în felul următor:

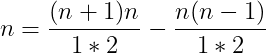
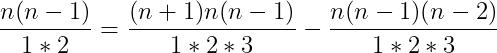
...
Continuând în aceeași manieră observăm că pot fi scriși coeficienții binomiali ai lui n în funcție de n+1.
Înlocuind în exprimarea factorului reprezentat de paranteza lungă din exprimarea lui z^n-x^n, putem să separăm exprimarea în funcție de coeficienții binomiali pentru exponentul n+1 și coeficienții binomiali pentru exponentul n.
Dezvoltând se ajunge generalizat la o exprimare de genul:
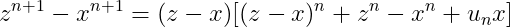
unde u_n este factorul reprezentat de "paranteza mare" din exprimarea lui z^n-x^n.
Exprimând z^(n+1)-x^(n+1) în aceeași manieră cum a fost exprimat z^n-x^n, simplificând cu (z-x) se ajunge la o exprimare identică doar cu exponentul crescut cu o unitate și indicele lui u crescut cu o unitate, aceasta putând fi considerată o relație de recurență generalizată.
Înlocuind tot timpul valorile lui u_n, u_(n-1), u_(n-2),... se ajunge la o exprimare interesantă.
Nu știu deocamdată la ce poate ajuta, dar am considerat că merită menționată în subiect.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Și totuși, și aici e o greșeală undeva.
Care nu duce la vreo concluzie concretă.
Undeva, în loc de (z-x) am scris x și schimbă tot.
Care nu duce la vreo concluzie concretă.
Undeva, în loc de (z-x) am scris x și schimbă tot.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
O lectura pentru curiosul :
https://pdfcoffee.com/unchiul-petros-si-conjectura-lui-goldbach-pdf-free.html
Si nu numai pentru el !
https://pdfcoffee.com/unchiul-petros-si-conjectura-lui-goldbach-pdf-free.html
Si nu numai pentru el !
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44567
Data de inscriere : 03/12/2013
 Re: Simetrie binomială
Re: Simetrie binomială
O știu, virgil_48, de fapt, am tratat cumva în subiectul ăla cu Lista lui Landau și conjectura lui Goldbach, și vreo alte 4 probleme referitoare la numerele prime.
Îmi amintesc că la acel moment ajunsesem la concluzia că mai mult de cât am analizat în acel subiect nu mai pot face.
În schimb, cred că i-am dat de capăt teoremei lui Fermat intr-un mod cât se poate de clar, cred.
Dar sunt la serviciu acum și o să scriu diseară.
Am tot reverificat coerența și corectitudinea în mintea mea și pare ok.
O să prezint diseară.
Îmi amintesc că la acel moment ajunsesem la concluzia că mai mult de cât am analizat în acel subiect nu mai pot face.
În schimb, cred că i-am dat de capăt teoremei lui Fermat intr-un mod cât se poate de clar, cred.
Dar sunt la serviciu acum și o să scriu diseară.
Am tot reverificat coerența și corectitudinea în mintea mea și pare ok.
O să prezint diseară.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Am văzut pe internet cartea https://booknation.ro/carti/carte-pdf.php?product_id=1191397.Sții ceva despre aceasta carte?curiosul a scris:O știu, virgil_48, de fapt, am tratat cumva în subiectul ăla cu Lista lui Landau și conjectura lui Goldbach, și vreo alte 4 probleme referitoare la numerele prime.
Îmi amintesc că la acel moment ajunsesem la concluzia că mai mult de cât am analizat în acel subiect nu mai pot face.
În schimb, cred că i-am dat de capăt teoremei lui Fermat intr-un mod cât se poate de clar, cred.
Dar sunt la serviciu acum și o să scriu diseară.
Am tot reverificat coerența și corectitudinea în mintea mea și pare ok.
O să prezint diseară.
Ce cărți ai care tratează Marea Teoremă a lui Fermat?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2602




Puncte : 22063
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Simetrie binomială
Re: Simetrie binomială
Dacă întrebarea mi se adresează, eu nu prea sunt cu cărțile, Dacule.
Am primit odată una, de teorie a numerelor, pe care am citit-o din scoarța în scoarța și o știu aproape pe de rost, și am cumpărat două, una de fizică atomică și un compendiu de matematică care trata mai mult inele și grupuri.
În rest, nu prea sunt cu cărțile.
Dar citesc destul de mult online subiecte care mă interesează.
Să văd ce am socotit azi în minte cu teorema lui Fermat.
Sper să fie corect.
Am primit odată una, de teorie a numerelor, pe care am citit-o din scoarța în scoarța și o știu aproape pe de rost, și am cumpărat două, una de fizică atomică și un compendiu de matematică care trata mai mult inele și grupuri.
În rest, nu prea sunt cu cărțile.
Dar citesc destul de mult online subiecte care mă interesează.
Să văd ce am socotit azi în minte cu teorema lui Fermat.
Sper să fie corect.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Și se pare că am dreptate în ce am scris în primele mesaje din acest topic.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Și "problema" este că chiar pot să demonstrez concluzia de pe pagina 5 din postările inițiale din acest topic.curiosul a scris:Și se pare că am dreptate în ce am scris în primele mesaje din acest topic.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Procedura în sine pe care se bazează demonstrația pe care cred că pot să o dezvolt se bazează în esența ei, pe faptul că în această "simetrie binomială", exprimând dezvoltarea în funcție de orice mod în care poate fi scris x+y ca orice sumă de a+b, dacă în acest tip de dezvoltare binomială se ajunge ca intr-o parte a egalității să fie exprimat în funcție de a, iar în cealaltă parte în funcție de o valoare diferită de b, dacă b1, b2, b3,...,bn, sunt toate diferite în același sens, adică toate mai mici sau toate mai mari, în mod consecutiv, decât valorile lui b, corespunzătoare exponentului său din dezvoltare, egalitatea nu poate fi posibilă.
Iar asta este demonstrabil și concluziile de pe paginile 4 și 5 expuse la început în subiect trebuie obligatoriu să fie adevărate.
Asta înseamnă clar că ecuația nu poate avea soluții intregi, naturale, pentru n>2.
Iar asta este demonstrabil și concluziile de pe paginile 4 și 5 expuse la început în subiect trebuie obligatoriu să fie adevărate.
Asta înseamnă clar că ecuația nu poate avea soluții intregi, naturale, pentru n>2.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
O să prezint în continuare o demonstrație pentru cazul n=3 bazată pe această simetrie binomială.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
Conform acestei simetrii binomiale, pentru n=3, în orice formă poate fi scris u=a+b se ajunge la relația:

Se poate exprima suma x+y în două moduri diferite,
(x+y)=x+y și (x+y)=z+(x+y-z)
Aplicând relația de mai sus pentru fiecare caz în parte se ajunge la
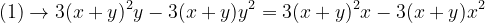
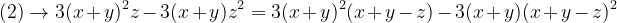
În relația (1) trecem membrii din dreapta în stânga și rescriem relația sub forma
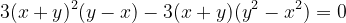
unde notăm

și rescriem relația anterioară

Desfacem relația aducând-o la forma

Corelat cu relația (2) putem scrie
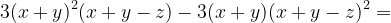
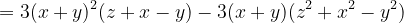
Egalitatea de mai sus o putem scrie simplificat sub forma
ab-cd=ab'-cd'
În numere naturale această egalitate implică exprimarea lui b' și d' obligatoriu sub forma:
b' = (b + uc) și d' = (d + ua)
cu u natural mai mare sau egal cu 0.
Înlocuind acest aspect în ultima relație trebuie să avem egalitățile:

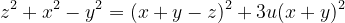
Din prima relație se ajunge la 3u(x+y)=2(z-y)
Dacă x, y, z sunt soluții naturale prime intre ele ale ecuației x^3+y^3=z^3, atunci (x+y) este factorul lui z^3, iar (z-y) este factorul lui x^3.
z și x fiind prime între ele, (x+y) și (z-y) nu pot avea factori comuni, deși în egalitatea 3u(x+y)=2(z-y) factorizarea lui (x+y) trebuie să se regăsească complet în 2(z-y), ceea ce înseamnă că x și z nu pot fi prime între ele.
Pentru a generaliza cazul n>2 se poate demonstra in mod asemănător că prin această simetrie binomială x, y, z ca și soluții ale ecuației x^n+y^n=z^n nu pot fi soluții prime între ele.

Se poate exprima suma x+y în două moduri diferite,
(x+y)=x+y și (x+y)=z+(x+y-z)
Aplicând relația de mai sus pentru fiecare caz în parte se ajunge la
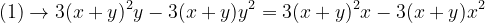
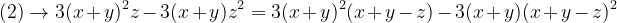
În relația (1) trecem membrii din dreapta în stânga și rescriem relația sub forma
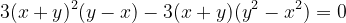
unde notăm

și rescriem relația anterioară

Desfacem relația aducând-o la forma

Corelat cu relația (2) putem scrie
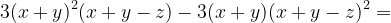
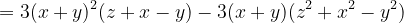
Egalitatea de mai sus o putem scrie simplificat sub forma
ab-cd=ab'-cd'
În numere naturale această egalitate implică exprimarea lui b' și d' obligatoriu sub forma:
b' = (b + uc) și d' = (d + ua)
cu u natural mai mare sau egal cu 0.
Înlocuind acest aspect în ultima relație trebuie să avem egalitățile:

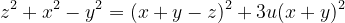
Din prima relație se ajunge la 3u(x+y)=2(z-y)
Dacă x, y, z sunt soluții naturale prime intre ele ale ecuației x^3+y^3=z^3, atunci (x+y) este factorul lui z^3, iar (z-y) este factorul lui x^3.
z și x fiind prime între ele, (x+y) și (z-y) nu pot avea factori comuni, deși în egalitatea 3u(x+y)=2(z-y) factorizarea lui (x+y) trebuie să se regăsească complet în 2(z-y), ceea ce înseamnă că x și z nu pot fi prime între ele.
Pentru a generaliza cazul n>2 se poate demonstra in mod asemănător că prin această simetrie binomială x, y, z ca și soluții ale ecuației x^n+y^n=z^n nu pot fi soluții prime între ele.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
De regulă, nici eu nu prea am încredere în obiectivitatea concluziilor ce tocmai eu pot să le deduc, motiv pentru care nu pot să accept un aspect din expunerea de mai sus, deși el respectă o anumită liniaritate logică.
Inconsistența de mai sus, raportat la x, y, z ca și soluții ale ecuației x^3+y^3=z^3 se referă la aceea valoare a lui u, care se pare că el trebuie obligatoriu să fie rațional, nu întreg.
Dar dacă u este rațional, fie z+x-y nu poate fi întreg, fie trebuie să avem corespondențele k_1 =x+y-z, k_2= (x+y-z)^2, etc, exact așa cum am anticipat incomplet demonstrat în primele mesaje din topic.
Inconsistența de mai sus, raportat la x, y, z ca și soluții ale ecuației x^3+y^3=z^3 se referă la aceea valoare a lui u, care se pare că el trebuie obligatoriu să fie rațional, nu întreg.
Dar dacă u este rațional, fie z+x-y nu poate fi întreg, fie trebuie să avem corespondențele k_1 =x+y-z, k_2= (x+y-z)^2, etc, exact așa cum am anticipat incomplet demonstrat în primele mesaje din topic.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Simetrie binomială
Re: Simetrie binomială
De atâtea ori ai spus ba că e greșit ba că nu e greșit, ba că n trebuie sa fie impar ba că n poate fi și par încât nu se mai înțelege nimic.Te rog frumos dă odată demonstrația completă și formulele să le scrii cu https://arachnoid.com/latex/ în modul CodeCogs ca să putem urmări cursiv raționamentul tău și eventual să punem întrebări de clarificare.Nu uita să specifici clar dacă numerele x,y,z fac parte din mulțimea numerelor întregi nenule sau din mulțimea numerelor naturale nenule.curiosul a scris:Procedura în sine pe care se bazează demonstrația pe care cred că pot să o dezvolt se bazează în esența ei, pe faptul că în această "simetrie binomială", exprimând dezvoltarea în funcție de orice mod în care poate fi scris x+y ca orice sumă de a+b, dacă în acest tip de dezvoltare binomială se ajunge ca intr-o parte a egalității să fie exprimat în funcție de a, iar în cealaltă parte în funcție de o valoare diferită de b, dacă b1, b2, b3,...,bn, sunt toate diferite în același sens, adică toate mai mici sau toate mai mari, în mod consecutiv, decât valorile lui b, corespunzătoare exponentului său din dezvoltare, egalitatea nu poate fi posibilă.
Iar asta este demonstrabil și concluziile de pe paginile 4 și 5 expuse la început în subiect trebuie obligatoriu să fie adevărate.
Asta înseamnă clar că ecuația nu poate avea soluții intregi, naturale, pentru n>2.
----------------------------------------
Dacă alegi x,y,z mulțimea numerelor naturale nenule te rog să specifici relația de ordine între numerele x,y,z și firesc ar fi ca această să fie x mai mic ca y mai mic ca z.
Dacă alegi mulțimea numerelor întregi vei vedea că este mult mai dificil să găsești o demonstrație.
---------------------------------------
Dacă crezi că ai găsit demonstrația, atunci publică această demonstrație scriind o carte și/sau ia legătura cu secția cu Secția de Științe Matematice de la Academia Română și în acest sens vezi https://acad.ro/institutia/sectii.html.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2602




Puncte : 22063
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
Pagina 1 din 2 • 1, 2 
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|




 Devino fan Forumgratuit
Devino fan Forumgratuit 









