Ultimele subiecte
» Impulsul elicoidalScris de virgil Joi 25 Iul 2024, 17:43
» New topic
Scris de virgil Mier 24 Iul 2024, 07:33
» Ce fel de popor suntem
Scris de CAdi Mar 23 Iul 2024, 22:12
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Mar 23 Iul 2024, 06:47
» Fenomene Electromagnetice
Scris de eugen Lun 22 Iul 2024, 21:37
» Sa mai auzim si de bine in Romania :
Scris de virgil Lun 22 Iul 2024, 18:39
» Masina Timpului
Scris de CAdi Lun 22 Iul 2024, 13:17
» Globalizarea
Scris de virgil Dum 21 Iul 2024, 16:46
» Unde a ajuns stiinta ?
Scris de CAdi Dum 21 Iul 2024, 15:20
» Ce este FOIP?
Scris de Abel Cavaşi Vin 19 Iul 2024, 22:02
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de CAdi Joi 18 Iul 2024, 11:51
» Inertia
Scris de virgil Mier 17 Iul 2024, 11:09
» Lucrul mecanic - definitie si exemple (Secţiunea 2)
Scris de CAdi Mar 16 Iul 2024, 05:20
» Laborator-sa construim impreuna
Scris de eugen Lun 15 Iul 2024, 10:17
» Stanley A. Meyer - Hidrogen
Scris de eugen Dum 14 Iul 2024, 20:25
» Despre vise
Scris de CAdi Sam 13 Iul 2024, 15:09
» Constatari
Scris de curiosul Sam 13 Iul 2024, 10:13
» Pendulul
Scris de virgil_48 Lun 08 Iul 2024, 16:18
» Marea teorema a lui Fermat.
Scris de curiosul Sam 06 Iul 2024, 10:23
» Legi de conservare (2)
Scris de Vizitator Vin 05 Iul 2024, 13:24
» PROFILUL CERCETATORULUI...
Scris de virgil Dum 30 Iun 2024, 19:01
» Grup de cercetare pentru constiinta
Scris de curiosul Sam 29 Iun 2024, 16:06
» CURIOZITATI; Motor miniatural functional
Scris de virgil Vin 28 Iun 2024, 20:36
» Fizicieni care au schimbat lumea.
Scris de eugen Vin 28 Iun 2024, 09:58
» O proprietate Black Hole (Gaura Neagra)
Scris de virgil Joi 27 Iun 2024, 17:58
» Cum marim energia atomului ?
Scris de virgil Dum 23 Iun 2024, 19:11
» Bec Tapo L530E 2.0 - Smart Wi-Fi Light Bulb, Multicolor
Scris de Dacu Vin 21 Iun 2024, 18:30
» Caracteristicile tehnice ale motoarelor auto
Scris de CAdi Joi 20 Iun 2024, 12:24
» Concluzii asupra relativității
Scris de curiosul Dum 16 Iun 2024, 11:55
» EMINESCU, Templu National
Scris de eugen Sam 15 Iun 2024, 22:29
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT... ( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la virgil în Sa mai auzim si de bine in Romania :
( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 2 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12347) | ||||
| CAdi (12205) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7950) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6162) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3889) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 39 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 39 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
A doua conjectură Hardy-Littlewood
2 participanți
Pagina 1 din 1
 A doua conjectură Hardy-Littlewood
A doua conjectură Hardy-Littlewood
Deși se consideră ca fiind neadevărată, sau cel puțin inconsistentă cu prima conjectură Hardy-Littlewood, această a doua conjectură H-L este foarte probabil adevărată.
O scurtă descriere, în engleză din păcate, găsiți pe wikipedia aici.
Aceasta presupune că inegalitatea\leq&space;\pi&space;(x)+\pi&space;(y)) este adevărată, unde
este adevărată, unde ,&space;\pi&space;(y),&space;\pi&space;(x+y)) reprezintă notațiile prin care se înțelege numărul de numere prime mai mici sau egale cu x, y și respectiv (x+y).
reprezintă notațiile prin care se înțelege numărul de numere prime mai mici sau egale cu x, y și respectiv (x+y).
În analiza de mai jos este dezvoltat raționamentul din care reiese concluzia la care am ajuns eu și anume, conjectura este foarte probabil adevărată.
1. Dacă un număr m, mai mic ca n, nu este prim, atunci el este obligatoriu divizibil cu cel puțin un număr prim mai mic sau egal cu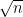 .
.
Evident, presupunând că acel număr m nu este prim și în același timp nedivizibil cu niciun număr prim mai mic sau egal cu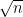 , atunci el va fi divizibil cu cel puțin două numere prime p,q mai mari decât
, atunci el va fi divizibil cu cel puțin două numere prime p,q mai mari decât 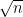 , ceea ce ar însemna că pq>n și evident m ar fi mai mare ca n, iar asta este imposibil, de unde rezultă că m trebuie să fie obligatoriu divizibil cu cel puțin un număr prim mai mic sau egal cu
, ceea ce ar însemna că pq>n și evident m ar fi mai mare ca n, iar asta este imposibil, de unde rezultă că m trebuie să fie obligatoriu divizibil cu cel puțin un număr prim mai mic sau egal cu 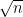 .
.
2. În intervalul (0,k) sunt cel puțin la fel de multe numere prime ca și în intervalul (y, y+k).
Evident, în cele două intervale sunt același număr de numere consecutive, cu diferența că în intervalul (0,k) numerele nonprime sunt divizibile cu cel puțin un număr prim mai mic sau egal cu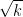 , în timp ce în al doilea interval, în factorizarea numerelor compuse apar numere prime mai mici sau egale cu
, în timp ce în al doilea interval, în factorizarea numerelor compuse apar numere prime mai mici sau egale cu 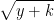 așa cum rezultă din 1.
așa cum rezultă din 1.
Aceasta înseamnă că în cele două intervale identice ca și număr de numere consecutive, există un număr diferit de numere prime care pot divide numerele nonprime, dacă y este suficient de mare.
Altfel spus, în cele două intervale există același număr de numere divizibile cu 2, același număr de numere divizibile cu 3,..., același număr de numere divizibile cu p prim mai mic sau egale cu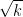 , însă în intervalul (y, y+k) mai pot apărea numere divizibile cu un număr prim cuprins între
, însă în intervalul (y, y+k) mai pot apărea numere divizibile cu un număr prim cuprins între 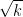 și
și 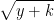 , de unde ar rezulta că în intervalul (y, y+k) ar putea fi mai puține numere prime decât în intervalul (0,k).
, de unde ar rezulta că în intervalul (y, y+k) ar putea fi mai puține numere prime decât în intervalul (0,k).
3. Din 2. rezultă faptul că-\pi&space;(y)\leq&space;\pi&space;(k)=\pi&space;((y+k)-y))
Înlocuind x=y+k, inegalitatea-\pi&space;(y)\leq&space;\pi&space;(x-y)) este foarte probabil adevărată pentru oricare x, y.
este foarte probabil adevărată pentru oricare x, y.
4. Rearanjând ultima inegalitate sub forma\leq&space;\pi&space;(x-y)+\pi&space;(y)) și notănd x-y=z și implicit x=z+y ajungem la
și notănd x-y=z și implicit x=z+y ajungem la \leq&space;\pi&space;(z)+\pi&space;(y)) adică exact ceea ce ar trebui demonstrat pentru a valida conjectura, însă trebuie o demonstrație mai riguroasă pentru punctul 2.
adică exact ceea ce ar trebui demonstrat pentru a valida conjectura, însă trebuie o demonstrație mai riguroasă pentru punctul 2.
Vreo idee?
O scurtă descriere, în engleză din păcate, găsiți pe wikipedia aici.
Aceasta presupune că inegalitatea
În analiza de mai jos este dezvoltat raționamentul din care reiese concluzia la care am ajuns eu și anume, conjectura este foarte probabil adevărată.
1. Dacă un număr m, mai mic ca n, nu este prim, atunci el este obligatoriu divizibil cu cel puțin un număr prim mai mic sau egal cu
Evident, presupunând că acel număr m nu este prim și în același timp nedivizibil cu niciun număr prim mai mic sau egal cu
2. În intervalul (0,k) sunt cel puțin la fel de multe numere prime ca și în intervalul (y, y+k).
Evident, în cele două intervale sunt același număr de numere consecutive, cu diferența că în intervalul (0,k) numerele nonprime sunt divizibile cu cel puțin un număr prim mai mic sau egal cu
Aceasta înseamnă că în cele două intervale identice ca și număr de numere consecutive, există un număr diferit de numere prime care pot divide numerele nonprime, dacă y este suficient de mare.
Altfel spus, în cele două intervale există același număr de numere divizibile cu 2, același număr de numere divizibile cu 3,..., același număr de numere divizibile cu p prim mai mic sau egale cu
3. Din 2. rezultă faptul că
Înlocuind x=y+k, inegalitatea
4. Rearanjând ultima inegalitate sub forma
Vreo idee?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: A doua conjectură Hardy-Littlewood
Re: A doua conjectură Hardy-Littlewood

PI(x) < PI(x+k) < PI(x)+PI(k)
De la un nr oarecare PI(x) aproximeaza(aproximatiile se reduc cu atit mai mult cu cit dam valori mai mari) o functie concava crescatoare, la fel si PI(x+k) la fel si PI(x)+PI(k). Nici una din cele 3 functii nu se intersecteaza dupa un anumit numar in sus, deci e deajuns sa dam 2,3 exemple sa le comparam si imedeat deci sa aflam care functie e mai mare sau mai mica ca cealalta.
Hercules- Statornic

- Mulţumit de forum : Numarul mesajelor : 52




Puncte : 8871
Data de inscriere : 20/07/2016
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: A doua conjectură Hardy-Littlewood
Re: A doua conjectură Hardy-Littlewood
Da Hercules, eu înțeleg cam ce vrei să spui.
Oricum, o să revin zilele astea cu un raționament mult mai plauzibil și mai detaliat, care validează conjectura.
Discutăm ulterior.
Oricum, o să revin zilele astea cu un raționament mult mai plauzibil și mai detaliat, care validează conjectura.
Discutăm ulterior.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: A doua conjectură Hardy-Littlewood
Re: A doua conjectură Hardy-Littlewood
Interesant, Hercules, este că oricare una dintre cele două relații de mai jos este adevărată o implică pe cealaltă :
\leq&space;\pi&space;(x)+\pi&space;(y))
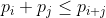
unde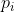 este al i-lea nr prim.
este al i-lea nr prim.
unde
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: A doua conjectură Hardy-Littlewood
Re: A doua conjectură Hardy-Littlewood
A doua conjectura H-L și anume, \leq \pi (x)+\pi (y)}) nu este tocmai echivalentă cu
nu este tocmai echivalentă cu  pentru că prima relație o implică pe a doua, însă nu găsesc totuși un raționament corect, deocamdată cel puțin, care să implice prima relație considerând adevărată a doua relație.
pentru că prima relație o implică pe a doua, însă nu găsesc totuși un raționament corect, deocamdată cel puțin, care să implice prima relație considerând adevărată a doua relație.
Mai jos, un raționament care arată cum rezultă a doua relație din prima.
Orice număr n>2 poate fi încadrat între două numere prime consecutive astfel încât . În acest fel putem încadra x și y în relațiile
. În acest fel putem încadra x și y în relațiile  și
și  .
.
De aici reultă că și implicit faptul că
și implicit faptul că  \leq \pi (x+y)}) .
.
Dacă înlocuim=i}) și
și =j}) și considerând că relația
și considerând că relația \leq \pi (x)+\pi (y)}) este adevărată, ar însemna de asemenea că
este adevărată, ar însemna de asemenea că \leq \pi (p_{i})+\pi (p_{j})}) , iar înlocuind valorile de mai sus inegalitatea devine
, iar înlocuind valorile de mai sus inegalitatea devine \leq i+j}) .
.
Însă i+j poate fi scris sub forma= i+j}) și înlocuind din nou se ajunge la
și înlocuind din nou se ajunge la \leq \pi (p_{i+j})}) ceea ce ar însemna evident că
ceea ce ar însemna evident că  .
.
De aici se deduce faptul că dacă relația\leq \pi (x)+\pi (y)}) este adevărată, atunci este adevărată și relația
este adevărată, atunci este adevărată și relația  .
.
Mai jos, un raționament care arată cum rezultă a doua relație din prima.
Orice număr n>2 poate fi încadrat între două numere prime consecutive astfel încât
De aici reultă că
Dacă înlocuim
Însă i+j poate fi scris sub forma
De aici se deduce faptul că dacă relația
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Subiecte similare
Subiecte similare» Două probleme interesante
» Un numar natural de doua cifre...
» Două corpuri cu temperaturi diferite
» Un numar natural de doua cifre...
» Două corpuri cu temperaturi diferite
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|




 Devino fan Forumgratuit
Devino fan Forumgratuit 