Ultimele subiecte
» În ce tip de dovezi aveţi încredere deplină?Scris de virgil Astazi la 11:31
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Astazi la 10:33
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 12:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 04:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 03:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 10:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 00:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 00:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 09:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 11:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 02:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 06:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 01:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mar 05 Noi 2024, 22:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 10:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 01:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 11:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 04:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 12:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 03:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 12:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 06:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 02:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 14:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 14:03
» Despre credinţă şi religie
Scris de Dacu2 Mar 22 Oct 2024, 23:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 03:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 03:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 14:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 12:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la eugen în Global warming is happening?
( 1 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 14 utilizatori conectați: 1 Înregistrați, 0 Invizibil și 13 Vizitatori :: 1 Motor de căutareForever_Man
Recordul de utilizatori conectați a fost de 181, Joi 25 Ian 2024, 16:57
Subiecte similare
Conjectura lui Andrica
+2
Abel Cavaşi
curiosul
6 participanți
Pagina 3 din 7
Pagina 3 din 7 •  1, 2, 3, 4, 5, 6, 7
1, 2, 3, 4, 5, 6, 7 
 Conjectura lui Andrica
Conjectura lui Andrica
Rezumarea primului mesaj :
...
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 06:44, editata de 3 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
pun și purcelușul! cu cardiogramele complete de la k=1 la k=5

docs.google.com - serii_conjectura_lui_andrica
numai așa merge imaginea full că a obosit netul cînd am încercat să îi bag pe gît ditamai poza!

docs.google.com - serii_conjectura_lui_andrica
numai așa merge imaginea full că a obosit netul cînd am încercat să îi bag pe gît ditamai poza!
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
Se spune că prin anul 2000 s-a verificat ca fiind adevărată conjectura lui Andrica cu ajutorul calculatorului pentru toate numerele prime mai mici ca numărul  .Intuiţia mea îmi spune că trebuie să existe totuşi multe perechi de numere prime consecutive care nu respectă conjectura lui Andrica deoarece este ştiut faptul că din conjectura lui Bertrand
.Intuiţia mea îmi spune că trebuie să existe totuşi multe perechi de numere prime consecutive care nu respectă conjectura lui Andrica deoarece este ştiut faptul că din conjectura lui Bertrand  rezultă că
rezultă că  ceea ce înseamnă că cel mult poate exista între anumite numere prime relaţia
ceea ce înseamnă că cel mult poate exista între anumite numere prime relaţia  şi în acest caz dacă este adevărată concluzia mea şi anume "Dacă
şi în acest caz dacă este adevărată concluzia mea şi anume "Dacă  este al
este al  -lea număr prim pozitiv, atunci
-lea număr prim pozitiv, atunci  pentru orice
pentru orice  ." atunci rezultă că există numere prime consecutive pentru care de fapt este adevărat că
." atunci rezultă că există numere prime consecutive pentru care de fapt este adevărat că  pentru anumite valori ale lui
pentru anumite valori ale lui  ceea ce invalidează conjectura lui Andrica adică această conjectură nu este valabilă pentru toate perechile de numere prime consecutive existente.
ceea ce invalidează conjectura lui Andrica adică această conjectură nu este valabilă pentru toate perechile de numere prime consecutive existente.
Care este cea mai mare diferenţă de două numere prime consecutive cunoscută până azi?Pot exista două numere prime consecutive astfel încat diferenţa lor şi anume să fie suficient de mare astfel încât
să fie suficient de mare astfel încât  ?Greşesc eu cumva raţionamentul?Mulţumesc!
?Greşesc eu cumva raţionamentul?Mulţumesc!
Care este cea mai mare diferenţă de două numere prime consecutive cunoscută până azi?Pot exista două numere prime consecutive astfel încat diferenţa lor şi anume
Dacu- Foarte activ

- Numarul mesajelor : 2613
Data de inscriere : 28/07/2012
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
păi din seriile calculate la repezeală de mine, pentru n=[1;300] și k=[1;5] nici nu e adevărată în sens absolut, adică ∀(n,k)∈ℕ* ⋀ pₙ∈ℙ ⤇ a=p₍ₙ₊ₖ₎ ⋀ b=pₙ, pentru k>1!
contraexemplele apar chiar la început și cu cît crește k cu atît sunt mai multe într-un fel de creștere exponențială la capul de serie!
dar tot la fel de repede, pentru fiecare k, șirul începe să se stabilizeze în intervalul [k,k-1] și cu cît n e mai mare parcă șirul tinde asimptotic spre k!
dar nu depășește k! cum spui și tu posibil și pentru k>1 pînă la valori enorme pentru n+k!
variațiile în valoare absolută între termenii consecutivi ai unei serii devin tot mai mici, se atenuează, nu cresc! și asta duce la aparența de limită asimptotică clasică, ca un fel de logaritm cu creștere monotonă, leeentă, dar bine delimitată!
e foarte interesantă cardiograma aia! felul în care se comportă ca o limită asimptotică! cum seriile numerice pentru fiecare k urmăresc seriile anterioare, fiecare variație, fiecare vălurile, deal și vale, depresiune și urcuș, dar nu perfect identic!
că dacă ar fi variație identică ar fi trebuit să se încadreze în în intervalul [k,k-1] urmărind fidel variațiile pentru seria k=1 toate celelalte serii cu k>1!
deci acolo avem de fapt o frecvență ascunsă într-o altă frecvență mai mare!
dacă mă iau băbește după cardiogramele alea aș putea emite empiric ipoteza că mediile aritmetice chiar devin liniile k pentru n→∞!
e suficient să le privești de la o distanță mai mare și deja, de la n=300 par cît se poate de drepte! exact k!
LE:
evident n-a durat mult și am coafat cazurile excepționale!
upgradarea cu și mai mult talent a conjecturii ar putea fi
∀(n,k)∈ℕ* ⋀ (pₙ,p₍ₙ₊ₖ₎)∈ℙ ⤇ 1 > ⁽ᵏ⁺¹⁾√p₍ₙ₎ - ⁽ᵏ⁺¹⁾√p₍ₙ₊ₖ₎ + 1 > 0
adică pentru p₍ₙ₊₁₎ e sqrt(2), p₍ₙ₊₂₎ e sqrt(3), p₍ₙ₊₃₎ e sqrt(4), p₍ₙ₊ₖ₎ e sqrt(k+1) și se încadrează iar strict în interval
sau, altfel spus:
∀(n,k)∈ℕ* ⋀ (pₙ,p₍ₙ₊ₖ₎)∈ℙ ⤇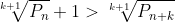
contraexemplele apar chiar la început și cu cît crește k cu atît sunt mai multe într-un fel de creștere exponențială la capul de serie!
dar tot la fel de repede, pentru fiecare k, șirul începe să se stabilizeze în intervalul [k,k-1] și cu cît n e mai mare parcă șirul tinde asimptotic spre k!
dar nu depășește k! cum spui și tu posibil și pentru k>1 pînă la valori enorme pentru n+k!
variațiile în valoare absolută între termenii consecutivi ai unei serii devin tot mai mici, se atenuează, nu cresc! și asta duce la aparența de limită asimptotică clasică, ca un fel de logaritm cu creștere monotonă, leeentă, dar bine delimitată!
e foarte interesantă cardiograma aia! felul în care se comportă ca o limită asimptotică! cum seriile numerice pentru fiecare k urmăresc seriile anterioare, fiecare variație, fiecare vălurile, deal și vale, depresiune și urcuș, dar nu perfect identic!
că dacă ar fi variație identică ar fi trebuit să se încadreze în în intervalul [k,k-1] urmărind fidel variațiile pentru seria k=1 toate celelalte serii cu k>1!
deci acolo avem de fapt o frecvență ascunsă într-o altă frecvență mai mare!
dacă mă iau băbește după cardiogramele alea aș putea emite empiric ipoteza că mediile aritmetice chiar devin liniile k pentru n→∞!
e suficient să le privești de la o distanță mai mare și deja, de la n=300 par cît se poate de drepte! exact k!
LE:
evident n-a durat mult și am coafat cazurile excepționale!
upgradarea cu și mai mult talent a conjecturii ar putea fi
∀(n,k)∈ℕ* ⋀ (pₙ,p₍ₙ₊ₖ₎)∈ℙ ⤇ 1 > ⁽ᵏ⁺¹⁾√p₍ₙ₎ - ⁽ᵏ⁺¹⁾√p₍ₙ₊ₖ₎ + 1 > 0
adică pentru p₍ₙ₊₁₎ e sqrt(2), p₍ₙ₊₂₎ e sqrt(3), p₍ₙ₊₃₎ e sqrt(4), p₍ₙ₊ₖ₎ e sqrt(k+1) și se încadrează iar strict în interval
sau, altfel spus:
∀(n,k)∈ℕ* ⋀ (pₙ,p₍ₙ₊ₖ₎)∈ℙ ⤇
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
de fapt dacă stau strîmb și mă scobesc un pic în nas îmi dau seama că n-am făcut altceva decît să descopăr că apa e udă:
dacă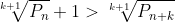 e adevărat atunci
e adevărat atunci 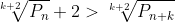 e cu atît mai mult adevărat!
e cu atît mai mult adevărat!
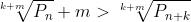 cînd m→∞ devine tot mai adevărat pentru că se transformă într-un banal 0 + m > 0
cînd m→∞ devine tot mai adevărat pentru că se transformă într-un banal 0 + m > 0
deci conjectura andrica generalizată e
∀(m,n,k)∈ℕ* ⋀ (pₙ,p₍ₙ₊ₖ₎)∈ℙ ⤇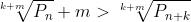
cu cît m crește cu atît e mai evident dpdv empiric că ar trebui să fie adevărată!
pentru k=0 și m=1 avem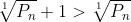 prin definiție adevărat!
prin definiție adevărat!
pare un start bun!
dacă
deci conjectura andrica generalizată e
∀(m,n,k)∈ℕ* ⋀ (pₙ,p₍ₙ₊ₖ₎)∈ℙ ⤇
cu cît m crește cu atît e mai evident dpdv empiric că ar trebui să fie adevărată!
pentru k=0 și m=1 avem
pare un start bun!
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
adică e de demonstrat faptul că din 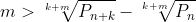 m crește tot timpul mai repede ca diferența dintre două numere m-consecutive băgate sub radical!
m crește tot timpul mai repede ca diferența dintre două numere m-consecutive băgate sub radical!
pentru m mare pare mai simplu ... pentru m mic, m=1 pare limita minimă de la care dacă coborîm mai jos nu mai e valabilă conjectura:
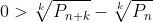 fals
fals
pentru m mare pare mai simplu ... pentru m mic, m=1 pare limita minimă de la care dacă coborîm mai jos nu mai e valabilă conjectura:
Ultima editare efectuata de catre totedati in Mier 14 Noi 2012, 12:08, editata de 1 ori
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:06, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
Ultima editare efectuata de catre totedati in Mier 14 Noi 2012, 12:44, editata de 1 ori
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
dacă mă iau după graficele funcției ![\sqrt[k+1]{P_{n+k}}-\sqrt[k+1]{P_{n}} + 1](http://latex.codecogs.com/gif.latex?\sqrt[k+1]{P_{n+k}}-\sqrt[k+1]{P_{n}} + 1)
cu cît k crește cu atît funcția anvelopează, e deasupra, celor cu k mai mic dar tot timpul sub 1!
în rare cazuri, la început, un k mai mic sare peste unul mai mare ca și cum ar fi inversul cardiogramei initiale, cînd tot la început în loc de intervalul [k,k-1] mai apăreau situații în care intervalul de variație era [k,k-2]
nu văd de ce dacă m crește peste 1 nu s-ar păstra trendul! atenuarea variațiilor ar trebui să fie și mai rapidă pînă la cazul maxim posibil 0 + (m→∞) > 0 care e un fel de apă udă
cu cît k crește cu atît funcția anvelopează, e deasupra, celor cu k mai mic dar tot timpul sub 1!
în rare cazuri, la început, un k mai mic sare peste unul mai mare ca și cum ar fi inversul cardiogramei initiale, cînd tot la început în loc de intervalul [k,k-1] mai apăreau situații în care intervalul de variație era [k,k-2]
nu văd de ce dacă m crește peste 1 nu s-ar păstra trendul! atenuarea variațiilor ar trebui să fie și mai rapidă pînă la cazul maxim posibil 0 + (m→∞) > 0 care e un fel de apă udă
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
Fără supărare,dar este greşit raţionamentul şi eu zic că este foarte posibil ca acea a doua inegalitate să fie adevărată dacă se raţionează în mod corect.Rog a se reciti cu atenţie ultima mea postare cu acea dublă inegalitate.curiosul a scris:Plec de la relatia pe care ai scris-o tu :
A doua inegalitate este gresita :
iar ridicand totul la patrat se obtine:
Putem scrie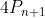
ca fiind,
iar inlocuind obtinem
si simplificand prin)
obtinem :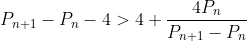
adica
Prin postulatul lui Bertrand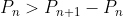
ceea ce inseamna ca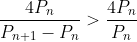
deci si
de unde rezulta ca
deci si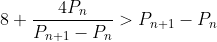
ceea ce inseamna ca,
precum si
Eu as spune chiar ca limitele sunt :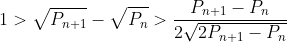
Eu zic că este foarte posibil să existe perechi de numere prime consecutive astfel încât
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22427
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
dacă p₍ₙ₊₁₎ - pₙ e suficient de mare p₍ₙ₊₂₎ - pₙ ar fi și mai mare! și dacă mărim distanța dintre numerele prime de la 1-consecutive la m-consecutive ajungem la concluzia inversă, că ar fi adevărată conjectura!
adică la 0 + (m→∞) > 0
adică la 0 + (m→∞) > 0
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
Fără supărare,dar de ce nu se scrie cu latex?Conjectura lui Andrica se referă doar la perechi de numere prime consecutive şi îmi pare rău dar nu înteleg ce vrea să se spună prin raţionamentul de mărire a acelei aşa zise distanţe dintre două numere prime.Dacă se face referire la numărul primtotedati a scris:dacă p₍ₙ₊₁₎ - pₙ e suficient de mare p₍ₙ₊₂₎ - pₙ ar fi și mai mare! și dacă mărim distanța dintre numerele prime de la 1-consecutive la m-consecutive ajungem la concluzia inversă, că ar fi adevărată conjectura!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22427
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:05, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
Ultima editare efectuata de catre totedati in Mier 14 Noi 2012, 13:24, editata de 2 ori
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:05, editata de 2 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
LOL!
ai uitat să permutezi radicalii!
adică din a-b<1 ⤇ b-a>1

păi ce știm e că
adică a>b
dar cum ai sărit la a>b>c e treaba ta, nu mă bag
că relația lui dacu nu spune că b>c! ci strict a>b!
ai uitat să permutezi radicalii!
adică din a-b<1 ⤇ b-a>1
păi ce știm e că
Dacu a scris:Trei inegalităţi privind numerele prime consecutive:
1) Dacăeste al
-lea număr prim pozitiv, atunci
pentru orice
.
adică a>b
dar cum ai sărit la a>b>c e treaba ta, nu mă bag
că relația lui dacu nu spune că b>c! ci strict a>b!
Ultima editare efectuata de catre totedati in Mier 14 Noi 2012, 13:28, editata de 1 ori
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:05, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
eu cred că ai obosit!
ia o pauză, o ceașcă de cafea și revin-o!
și mai uită-te pe ecuații după ce te-ai mai odihnit ...
ia o pauză, o ceașcă de cafea și revin-o!
și mai uită-te pe ecuații după ce te-ai mai odihnit ...
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:06, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:06, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
curiosul a scris:Eu asta am aratat !
Nu este corect ?
Inseamna ca incep sa am o problema.
eu n-am mai stat să analizez ce ai vrut să demonstrezi! ți-am arătat că din a-b>1 nu rezultă a-b<1 ci b-a<1
după care am mușcat cu poftă!
ham ham!
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
Ultima editare efectuata de catre totedati in Mier 14 Noi 2012, 14:29, editata de 1 ori
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
eu deaia tot spun că mi-e frică de inegalități! și prefer egalitățile în ecuații!
noi ca noi că mai greșim da' să îi vezi pe profi la tablă cum se fac de cacao!
noi ca noi că mai greșim da' să îi vezi pe profi la tablă cum se fac de cacao!
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 08:06, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41548
Data de inscriere : 22/03/2011
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Conjectura lui Andrica
Re: Conjectura lui Andrica
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
Pagina 3 din 7 •  1, 2, 3, 4, 5, 6, 7
1, 2, 3, 4, 5, 6, 7 
Pagina 3 din 7
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
