Conjectura lui Andrica

Rezumarea primului mesaj :

...

așa e
le sucesc de le amețesc!

dar intenția e de a găsi un fir pe care după ce ajung la banalitatea să îl parcurg invers, ca în romanele polițiste spre sursa problemei dar de data asta în siguranță, cu arma în mînă și lanterna aprinsă!

din k+m=g și

pentru k=g-m avem



pt. n+g-m=e avem



iar din g=e=n=a avem



adică



pt. a-1=k rezultă



dar deja știm că

deci ... se pare că avem două variate de a ajunge de la la

lol!

Dacu a scris:Cum se rezolvă inegalitatea şi cum se rezolvă inegalitatea ?Rog mult de tot a se reciti cu atenţie toate postările mele.Muţumesc!

păi cu numerele prime parcă ar fi așa:

din



și din



avem



însă cum Pₙ∈ℕ* ⤇ rezultă

eliminînd , o cantitate pozitivă, se schimbă semnul inecuației?

devine



sau nu?

pentru avem

dacă avem rezultă

dacă avem rezultă
deci cheia soluției stă în

dacă o elimin sau adaug cum se schimbă semnul!? nu pot avea egalitate decît într-un singur caz particular! e ori laie ori bălaie

și atunci din
P₍ₙ₊₁₎< 2∙Pₙ
P₍ₙ₊₁₎-PₙP₍ₙ₊₁₎-Pₙ=Pₙ-k unde și k∈ℕ*

iar valoarea maximă a lui (Pₙ-k) nu poate fi decît (Pₙ-1) pentru că un K=0 ar invalida P₍ₙ₊₁₎<2∙Pₙ

astfel ajungem la
P₍ₙ₊₁₎-Pₙ=Pₙ-1
P₍ₙ₊₁₎+1=2∙Pₙ

nu îmi dau seama cum ai ajuns la !
din

a=P₍ₙ₊₁₎
b=Pₙ
c=P₍ₙ₊₁₎-Pₙ

ecuația de mai sus devine un simplu



care mie îmi dă cu virgulă!

totedati a scris:nu îmi dau seama cum ai ajuns la !
din

a=P₍ₙ₊₁₎
b=Pₙ
c=P₍ₙ₊₁₎-Pₙ

Repet ceea ce am postat într-un mesaj anterior cu rugămintea de a citi cu atenţie ce am scris:
---------------------------------------------------
"Se spune că prin anul 2000 s-a verificat ca fiind adevărată conjectura lui Andrica cu ajutorul calculatorului pentru toate numerele prime mai mici ca numărul .Intuiţia mea îmi spune că trebuie să existe totuşi multe perechi de numere prime consecutive care nu respectă conjectura lui Andrica deoarece este ştiut faptul că din conjectura lui Bertrand rezultă că ceea ce înseamnă că cel mult poate exista între anumite numere prime relaţia şi în acest caz dacă este adevărată concluzia mea şi anume "Dacă este al -lea număr prim pozitiv, atunci pentru orice ." atunci rezultă că există numere prime consecutive pentru care de fapt este adevărat că pentru anumite valori ale lui ceea ce invalidează conjectura lui Andrica adică această conjectură nu este valabilă pentru toate perechile de numere prime consecutive existente.
Care este cea mai mare diferenţă de două numere prime consecutive cunoscută până azi?Pot exista două numere prime consecutive astfel încat diferenţa lor şi anume să fie suficient de mare astfel încât ?Greşesc eu cumva raţionamentul?Mulţumesc!"
--------------------------------------------------------------------------------------
Ce este neclar în raţionamentul meu?Am arătat foarte clar de ce şi în care caz ar fi posibilă acea inegalitate.Aştept lămuriri.Mulţumesc!

...

aha! acum m-am prins! din
a=P₍ₙ₊₁₎
b=Pₙ
c=P₍ₙ₊₁₎-Pₙ
rezultă


dacă

eu mă luptam degeaba cu cifra 1 greșită!


și atunci deoarece e adevărat ajungem la forma finală



dacă x>y și (x,y)∈ℕ* adică y>1 dar în același timp și x>y ⤇ x>y>1 și x>x/y>1

da ... înseamnă că expresia e adevărată pentru orice (a,c)∈ℕ* cu c>a

înseamnă că pentru a restrînge domeniul de definiție a lui c trebuie să creștem cît mai mult !
trebuie să căutăm perechea de numere (a,c)∈ℕ* pentru care pentru că atunci x>x/y devine x≥x/(y→1)

însă din a=P₍ₙ₊₁₎, b=Pₙ, c=P₍ₙ₊₁₎-Pₙ
avem a+c=P₍ₙ₊₁₎+P₍ₙ₊₁₎-Pₙ=2∙P₍ₙ₊₁₎-Pₙ
deci 2∙P₍ₙ₊₁₎-Pₙ→1 cînd (Pₙ⇆2∙P₍ₙ₊₁₎ )+1

atunci (Pₙ⇆2∙P₍ₙ₊₁₎ )+1 devine celebrul (Pₙ-1)⇆2∙P₍ₙ₊₁₎

cum Pₙ≠2∙P₍ₙ₊₁₎ pentru că Pₙ∈ℙ, adică e număr prim, cel mai mare Pₙ-k e cel mai mic 2∙P₍ₙ₊₁₎+k adică k=1 dacă ∈ℕ*

nu putem avea un alt k mai mare care să aducă mai aproape de 1 expresia (Pₙ⇆2∙P₍ₙ₊₁₎ )+k

da ... acum încep să înțeleg ce ai vrut să spui dacule!

e practic un postulat, o limită teoretică care rezultă din formularea problemei care se cere rezolvată!

no ... acum e acum! cum demonstăm că k=1 pentru orice n∈ℕ*!?

sau ...
din k→1 dacă și numai dacă n→∞ și k=1 dacă și numai dacă n=∞ rezultă k>1 ∀n∈ℕ* pentru că ∀Pn∈ℙ avem Pn<∞!?

sau altfel spus {ℙ}∩{∞}=∅ pentru că nici un număr prim nu e infinit de mare!

deci k>1, Pₙ-k<2∙P₍ₙ₊₁₎ ∀k∈ℕ*!

acuma asta îmi dă voie să sar de la Pₙ-k<2∙P₍ₙ₊₁₎ la Pₙ-1<2∙P₍ₙ₊₁₎ direct la Pₙ-1
păi de ce nu! raționamentul e identic! în loc de Pₙ<2∙P₍ₙ₊₁₎ mă folosesc de relația Pₙ
maximul expresiei P₍ₙ₊₁₎⇆2∙Pₙ e (P₍ₙ₊₁₎-k)⇆2∙Pₙ pentru că dacă k=0 aș avea P₍ₙ₊₁₎=2∙Pₙ fals în mulțimea numerelor prime!

înseamă că k>1 ∀k∈ℕ* !
înseamnă că P₍ₙ₊₁₎-k < 2∙Pₙ adică pentru k=1 NU există n∈ℕ* pentru care P₍ₙ₊₁₎-1 = 2∙Pₙ !!!!

deci

P₍ₙ₊₁₎-1 < 2∙Pₙ ∀n∈ℕ*

în același mod ar trebui să putem face saltul de la
P₍ₙ₊₁₎-1 < 2∙Pₙ ∀n∈ℕ*
la
∀n∈ℕ*

...

!? hmmm .... damn! dap ... ar mai trebui lucrat la c ...

da' nu-i bai că tehnica e aceeași! eu nu înțelegeam la ce e bună expresia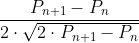 de ce ne-ar ajuta mai mult decît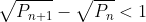

așa mi-am dat seama în ce fel vede el limitele și dinamica lor

așa cum am mai spus deja totul se reduce la a sări de la
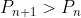și la care schimbă într-un mod profund datele problemei!

deși proporțiile date de m se păstrează ele sunt diferite pentru fiecare termen distinct al expresiei cu radicali!

se reduce proporțional cu m față de P₍ₙ₊₁₎! se reduce proporțional cu m față de Pₙ!

între și m încă menține o legătură de proporționalitate însă termenul k dă peste cap totul!

k nu e proporțional în nici un fel nici cu nici cu !

față de cei doi radicali se comportă ca o unitate infinită!
soluția sugerată de dacu e mult mai simplă ca strofocările mele și pare o direcție bună de a demonstra imposibilul ...

...

păi dacă e adevărată înseamnă că o putem demonstra!

O altă inegalitate privind numerele prime consecutive:
Dacă este al -lea număr prim pozitiv, atunci pentru orice .
Cum putem folosi această inegalitate pentru a verifica conjectura lui Andrica?Mulţumesc!

...

Cred că trebuie să ne lămurim altfel in ceea ce priveste conjectura lui Andrica.
In acest sens ar trebui să vedem cum rezolvăm următoarea inegalitate:
Să se rezolve inegalitatea unde , şi .
Aştept rezolvări.Mulţumesc!

...

...

Pornind de la inegalitatea rezultă că pot exista două cazuri şi anume:
1) şi

2) .

Din inegalitatea de la punctul 1) rezultă unde ceea ce înseamnă că ceea ce este foarte posibil.
Din inegalitatea de la punctul 2) rezultă unde ceea ce este foarte posibil.
În concluzie eu consider că dat fiind faptul că ceea ce înseamna că diferenţa poate fi oricât de mare atunci conjectura lui Andrica este posibil ca sa nu fie adevărata pentru toate toate perechile de numere prime consecutive .

Dacu a scris:În concluzie eu consider că dat fiind faptul că ceea ce înseamna că diferenţa poate fi oricât de mare atunci conjectura lui Andrica este posibil ca sa nu fie adevărata pentru toate toate perechile de numere prime consecutive .

hmm ... nu sunt sigur ... din P₍ₙ₊₁₎ - Pₙ < Pₙ nu rezultă tocmai afirmația inversă!? că Pₙ nu poate fi oricît de mare pentru că avem:

Pₙ < P₍ₙ₊₁₎, ∀ n∈ℕ*

deci Pₙ nu poate fi oricît de mare!

Dacă atunci cât de mare poate fi ?

bună întrebarea!

și eu am dat peste această problemă, faptul că din P₍ₙ₊₁₎ - Pₙ > 1 nu poți translata ușor la radicali diferența pentru că fiecare termen al șirului de sub radical scade în mod proporțional ȘI independent de ceilalți termeni ai șirului!

totedati a scris: se reduce proporțional cu m față de P₍ₙ₊₁₎! se reduce proporțional cu m față de Pₙ!

m=m îmi permite să translatez din P₍ₙ₊₁₎ > Pₙ în > însă doar atît, orice alt număr k în plus în ecuație îmi dă peste cap firul logic!

k nu e proporțional în nici un fel nici cu nici cu !

altă certitudine numerică e faptul că ceea ce se poate exprima și altfel, că , ∀(m,n)∈ℕ*!

oricît de mult cresc m și n nu pot trece sub 1 pentru că dacă x → ∞ avem !

pe teren avem situația pentru (m,n) → ∞ pentru că într-o astfel de situație avem

adică 1-1=0 limita de jos

adică din

putem spune că k>0 în orice situație! și atunci avem:
a) k>0 și k<1
b) k>0 și k>1
c) k>0 și k=1

varianta c e prima care cade, știm sigur că k≠1! mai rămîne k>1 sau k<1!
dacă m rămîne constant și crește n numerele de sub radical tind să crească tot mai mult, la fel diferența dintre ele dar din ce s-a calculat pînă acum avem tot timpul k<1!

cu cît crește mai mult m cu atît e mai sigur faptul că k<1!

înseamnă că pentru m=2 sunt cele mai mari șanse ca să avem un k > 1

cred că am reușit să demonstrez conjectura lui andrica!

din ∀ (n,k)∈ℕ* și (P₍ₙ₊₁₎,Pₙ)∈ℙ unde prin ℙ înțelegem mulțimea numerelor prime, dacă avem k>1 și Pₙ + k = P₍ₙ₊₁₎ atunci e adevărat că

Pₙ < P₍ₙ₊₁₎
Pₙ∙Pₙ < Pₙ∙P₍ₙ₊₁₎
(Pₙ)² < Pₙ∙P₍ₙ₊₁₎
(√Pₙ)² < √(Pₙ∙P₍ₙ₊₁₎) = √Pₙ∙√P₍ₙ₊₁₎
Pₙ < √Pₙ∙√P₍ₙ₊₁₎
2∙Pₙ < 2∙(√Pₙ∙√P₍ₙ₊₁₎)
2∙Pₙ - 2∙(√Pₙ∙√P₍ₙ₊₁₎) < 0
Pₙ + Pₙ - 2∙(√Pₙ∙√P₍ₙ₊₁₎) < 0
Pₙ + k + Pₙ - 2∙(√Pₙ∙√P₍ₙ₊₁₎) < k
(Pₙ + k)=P₍ₙ₊₁₎ + Pₙ - 2∙(√Pₙ∙√P₍ₙ₊₁₎) < k
P₍ₙ₊₁₎ + Pₙ - 2∙(√Pₙ∙√P₍ₙ₊₁₎) < k
P₍ₙ₊₁₎ + Pₙ - 2∙(√Pₙ∙√P₍ₙ₊₁₎) < √k∙√k
√P₍ₙ₊₁₎∙√P₍ₙ₊₁₎ - √Pₙ∙√P₍ₙ₊₁₎ - √P₍ₙ₊₁₎∙√Pₙ + (-√Pₙ)∙(-√Pₙ) < √k∙√k
(√P₍ₙ₊₁₎ - √Pₙ)² < (√k)²
√[(√P₍ₙ₊₁₎ - √Pₙ)²] < √[(√k)²]
√P₍ₙ₊₁₎ - √Pₙ < √k

de unde rezultă că

√P₍ₙ₊₁₎ < √k + √Pₙ sau altfel spus √Pₙ + √k > √P₍ₙ₊₁₎ !!!!

însă dacă √k > 1 pt. k > 1 cu atît mai mult k, pentru că avem k > √k > 1

deci √Pₙ + k > √P₍ₙ₊₁₎ ∀ (n,k)∈ℕ* ∧ (P₍ₙ₊₁₎,Pₙ)∈ℙ dacă k>1!
cum k=1 avem doar pentru P₁=2 și P₂=3 conjectura lui andrica devine adevărată prin demonstrația de mai sus pentru orice pereche de numere prime consecutive pentru că avem tot timpul √k > 1!

Conform postulatului lui Bertrand rezultă că ceea ce înseamnă că este foarte posibil ca şi deci în acest caz rezultă că dacă conjectura lui Andrica ar fi adevărată atunci ar trebui ca ceea ce presupune că ceea ce este fals pentru .
În concluzie rezultă că înainte de a demonstra conjectura lui Andrica trebuie mai întâi să vedem cât de mare poate fi diferenţa dintre două numere prime consecutive şi adică să vedem cât de mare poate fi .

de fapt n-am descoperit mare lucru, doar că pentru (a,b,c)∈ℕ* dacă a+b=c atunci √a + √b > √c

adică din Pₙ + k = P₍ₙ₊₁₎ atunci √Pₙ + √k > √P₍ₙ₊₁₎

ceea ce e în direcția cea bună dar de la √k pînă la 1 mai e ceva drum de parcurs ...

...

Repet:
"Conform postulatului lui Bertrand rezultă că ceea ce înseamnă că este foarte posibil ca şi deci în acest caz rezultă că dacă conjectura lui Andrica ar fi adevărată atunci ar trebui ca ceea ce presupune că ceea ce este fals pentru .
În concluzie rezultă că înainte de a demonstra conjectura lui Andrica trebuie mai întâi să vedem cât de mare poate fi diferenţa dintre două numere prime consecutive şi adică să vedem cât de mare poate fi ."
Trebuia să specific doar că relaţia este valabilă pentru .
Postulatul lui Bertrand spune că ceea ce este echivalent cu şi tocmai de aceea am spus ca este foarte posibil ca deoarece toate numerele prime mai mari ca sunt numere impare şi deci este foarte posibil ca .
-----------------------------
Care este relaţia de ordine a numerelor prime şi cum arătăm că şi cum ajungem de la această ultimă inegalitate la conjectura lui Andrica adică la ?

...