Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Ieri la 22:56
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în NEWTON
( 1 )
» Mesaj de la Meteorr în Global warming is happening?
( 1 )
» Mesaj de la eugen în În ce tip de dovezi aveţi încredere deplină?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 21 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 21 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Problema numerelor prime
+4
curiosul
joben
Iulian
Abel Cavaşi
8 participanți
Pagina 2 din 4
Pagina 2 din 4 •  1, 2, 3, 4
1, 2, 3, 4 
 Problema numerelor prime
Problema numerelor prime
Rezumarea primului mesaj :
Încă din adolescenţă am fost captivat de problema numerelor prime. Cineva mi-a spus că încă nu se cunoaşte cum sunt ordonate numerele prime, iar eu nu am vrut să-l cred că problema este chiar atât de complicată. Se pare că, totuşi, e.
Mai exact, fie dat şirul numerelor prime
Se pune problema de a stabili o legătură directă între numărul n şi numărul p. Cu alte cuvinte, dându-se numărul n, oricare ar fi acesta, să se determine al n-lea număr prim din şirul infinit al numerelor prime.
Cine va rezolva această problemă ne va da o formulă minunată care ne va permite să obţinem, de exemplu, din 7, 17 sau din 9, 23, etc.
Cândva, pe vremea când aveam mai mult timp liber, am găsit o soluţie la problema inversă: dându-se numărul prim p, să se găsească al câtelea număr prim este el în şirul numerelor prime. Dacă o voi găsi printre hârtiile mele vechi, o voi posta aici. Ştiu că era ceva cu partea întreagă a unui număr.
Vă doresc succes tuturor celor care se încumetă!
Încă din adolescenţă am fost captivat de problema numerelor prime. Cineva mi-a spus că încă nu se cunoaşte cum sunt ordonate numerele prime, iar eu nu am vrut să-l cred că problema este chiar atât de complicată. Se pare că, totuşi, e.
Mai exact, fie dat şirul numerelor prime
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... |
| p | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | ... |
Cine va rezolva această problemă ne va da o formulă minunată care ne va permite să obţinem, de exemplu, din 7, 17 sau din 9, 23, etc.
Cândva, pe vremea când aveam mai mult timp liber, am găsit o soluţie la problema inversă: dându-se numărul prim p, să se găsească al câtelea număr prim este el în şirul numerelor prime. Dacă o voi găsi printre hârtiile mele vechi, o voi posta aici. Ştiu că era ceva cu partea întreagă a unui număr.
Vă doresc succes tuturor celor care se încumetă!
 Re: Problema numerelor prime
Re: Problema numerelor prime
De unde iau programul "Maxima",caci nu inteleg cum il pot accesa?!?!
Iulian- Statornic

- Numarul mesajelor : 73
Data de inscriere : 12/05/2008
 Re: Problema numerelor prime
Re: Problema numerelor prime
Raspunde-mi te rog frumos?
Iulian- Statornic

- Numarul mesajelor : 73
Data de inscriere : 12/05/2008
 Re: Problema numerelor prime
Re: Problema numerelor prime
OT:
Ţi-am dat mai sus lincul spre Maxima.
E păcat că stricăm bunătate de topic .
.
EOT
Ţi-am dat mai sus lincul spre Maxima.
E păcat că stricăm bunătate de topic
EOT
 Re: Problema numerelor prime
Re: Problema numerelor prime
va sugerez sa studiati conjectura lui Andrica (prof. univ. in Cluj)
Ultima editare efectuata de catre joben in Dum 23 Mai 2010, 23:45, editata de 1 ori
_________________
"Un jucator bun este si norocos" (Capablanca)
joben- Preocupat

- Mulţumit de forum : Prenume : Robert




Numarul mesajelor : 35
Puncte : 18010
Data de inscriere : 22/05/2010
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Într-adevăr, ne putem mândri cu faptul că încă un român, chiar contemporan cu noi, a intrat în istoria matematicii formulând această conjectură simplă şi interesantă şi cine ştie cât de bogată în consecinţe. Mulţumim, joben, pentru semnalarea ei!
Mai departe, ar fi util aici să vedem în ce măsură conjectura lui Andrica, alături de multe alte conjecturi privind numerele prime, ar putea contribui la deducerea termenului general al şirului de numere prime.
Mai departe, ar fi util aici să vedem în ce măsură conjectura lui Andrica, alături de multe alte conjecturi privind numerele prime, ar putea contribui la deducerea termenului general al şirului de numere prime.
 Re: Problema numerelor prime
Re: Problema numerelor prime
asupra expresiei 2*3*5*...*p+1 ca ar fi numar prim nu sunt sigur (in orice caz n!+1 nu este prim intotdeauna ex. 4!+1=25), dar pentru demonstratia faptului ca sirul numerelor prime este infinit este utilizata expresia n!-1=nr prim care are o demonstratie la indemana prin reducere la absurdSpirala Numerelor Prime - Softpedia Forum
_________________
"Un jucator bun este si norocos" (Capablanca)
joben- Preocupat

- Mulţumit de forum : Prenume : Robert




Numarul mesajelor : 35
Puncte : 18010
Data de inscriere : 22/05/2010
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Iulian a scris :
"Te rog scrie-mi ce parere ai despre afirmatia mea:"Diferenta dintre oricare doua numere prime consecutive trebuie sa fie un numar mai mic decat un numar finit Zp,definit de mine ca fiind o constanta a sirului infinit de numere prime."
adresat lui Abel, intr-unul din mesajele de la inceputul acestui subiect.
Concluzia este demonstrabil gresita, Iulian, pentru ca diferenta dintre doua numere prime consecutive tinde catre infinit in jurul valorii
P(1)*p(2)*P(3)*...*P(n), daca P(n) tinde catre infinit.
Demonstratia ar fi urmatoarea:
In vecinatatea numarului P(1)*p(2)*P(3)*...*P(n), toate numerele cuprinse intre
[ P(1)*p(2)*P(3)*...*P(n) ] + 1 si
[ P(1)*p(2)*P(3)*...*P(n) ] + P(n+1),
cu exceptia acestora,
sunt numere care se divid cu un numar prim mai mic decat P(n+1), deci care nu sunt prime, ceea ce inseamna ca in vecinatatea numarului
P(1)*p(2)*P(3)*...*P(n) exista doua numere prime consecutive a caror diferenta este cel putin P(n+1)-1.
Pentru ca sunt o infinitate de numere prime, rezulta indirect ca daca P(n+1) tinde catre infinit, atunci diferenta dintre acele doua numere prime, din jurul valorii P(1)*p(2)*P(3)*...*P(n), tinde si ea catre infinit.
Deci Zp, constanta despre care vorbesti, nu este un numar finit, ci tinde catre infinit cu cat creste valoarea numarului prim P(n) din vecinatatea valorii P(1)*p(2)*P(3)*...*P(n).
"Te rog scrie-mi ce parere ai despre afirmatia mea:"Diferenta dintre oricare doua numere prime consecutive trebuie sa fie un numar mai mic decat un numar finit Zp,definit de mine ca fiind o constanta a sirului infinit de numere prime."
adresat lui Abel, intr-unul din mesajele de la inceputul acestui subiect.
Concluzia este demonstrabil gresita, Iulian, pentru ca diferenta dintre doua numere prime consecutive tinde catre infinit in jurul valorii
P(1)*p(2)*P(3)*...*P(n), daca P(n) tinde catre infinit.
Demonstratia ar fi urmatoarea:
In vecinatatea numarului P(1)*p(2)*P(3)*...*P(n), toate numerele cuprinse intre
[ P(1)*p(2)*P(3)*...*P(n) ] + 1 si
[ P(1)*p(2)*P(3)*...*P(n) ] + P(n+1),
cu exceptia acestora,
sunt numere care se divid cu un numar prim mai mic decat P(n+1), deci care nu sunt prime, ceea ce inseamna ca in vecinatatea numarului
P(1)*p(2)*P(3)*...*P(n) exista doua numere prime consecutive a caror diferenta este cel putin P(n+1)-1.
Pentru ca sunt o infinitate de numere prime, rezulta indirect ca daca P(n+1) tinde catre infinit, atunci diferenta dintre acele doua numere prime, din jurul valorii P(1)*p(2)*P(3)*...*P(n), tinde si ea catre infinit.
Deci Zp, constanta despre care vorbesti, nu este un numar finit, ci tinde catre infinit cu cat creste valoarea numarului prim P(n) din vecinatatea valorii P(1)*p(2)*P(3)*...*P(n).
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Am citit cam toate mesajele si am ajuns la urmatoarea parere:
Este interesant intr-adevar ca diferenta dintre doua numere prime consecutive este mai mica decat cel mai mic numar dintre cele doua numere prime adica daca p2>p1 atunci
Zp=p2-p1
Zp
Pe de alta parte s-ar putea ca aceasta diferenta Zp
Este interesant intr-adevar ca diferenta dintre doua numere prime consecutive este mai mica decat cel mai mic numar dintre cele doua numere prime adica daca p2>p1 atunci
Zp=p2-p1
Zp
Pe de alta parte s-ar putea ca aceasta diferenta Zp
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Vad ca nu s-a inregistrat corect mesajul si repet:
Am citit cam toate mesajele si am ajuns la urmatoarea parere:
Este interesant intr-adevar ca diferenta dintre doua numere prime consecutive este mai mica decat cel mai mic numar dintre cele doua numere prime adica daca p2>p1 atunci Zp=p2-p1 adica p1>p2-p1=Zp.
Este bineinteles ca desi aceasta diferenta Zp poate fi oricat de mare (zic unii) totusi p1>Zp
oricat de mare ar fi p1 si p2.
Pe de alta parte s-ar putea ca aceasta diferenta sa respecte inegalitatea p1>Cp>Zp unde Cp este o constanta a sirului
infinit de numere prime si mai afirm ca aceasta constanta Cp este un numar par.Cum am putea determina constanta Cp a sirului infinit de numere prime?
Am citit cam toate mesajele si am ajuns la urmatoarea parere:
Este interesant intr-adevar ca diferenta dintre doua numere prime consecutive este mai mica decat cel mai mic numar dintre cele doua numere prime adica daca p2>p1 atunci Zp=p2-p1 adica p1>p2-p1=Zp.
Este bineinteles ca desi aceasta diferenta Zp poate fi oricat de mare (zic unii) totusi p1>Zp
oricat de mare ar fi p1 si p2.
Pe de alta parte s-ar putea ca aceasta diferenta sa respecte inegalitatea p1>Cp>Zp unde Cp este o constanta a sirului
infinit de numere prime si mai afirm ca aceasta constanta Cp este un numar par.Cum am putea determina constanta Cp a sirului infinit de numere prime?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Pai sa le luam in ordine sa vedem unde nu am inteles corect.
In primul rand, relatia p1>p2-p1 se demonstreaza prin Teorema Bertrand-Chebasev , in felul urmator:
(daca p1,p2 tu le consideri doua numere prime consecutive, atunci le voi rescrie la termenul general, adica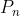 si
si 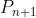 .)
.)
Prin aceasta teorema se demonstreaza ca intre x si 2x exista cel putin un numar prim.
Deci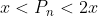
Considerand x ca fiind numarul prim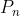 rezulta ca este adevarata relatia :
rezulta ca este adevarata relatia :
 , deci si
, deci si  atat timp cat
atat timp cat 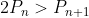 .
.
In ceea ce priveste : "...ca desi aceasta diferenta Zp poate fi oricat de mare (zic unii)..."
Nu zic unii, ci mai degraba o demonstreaza "unii" in felul urmator :
+1) nu se divide cu niciunul din numerele prime
nu se divide cu niciunul din numerele prime 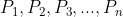
+2) se divide cu 2,
se divide cu 2,
+3) se divide cu 3,
se divide cu 3,
+4) se divide cu 2,
se divide cu 2,
etc.
Orice numar mai mic decat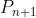 este fie un numar care se divide cu un numar prim mai mic decat
este fie un numar care se divide cu un numar prim mai mic decat 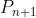 , fie un numar prim mai mic decat
, fie un numar prim mai mic decat 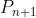 .
.
Asta inseamna ca adunand oricare numar mai mare ca 1 si mai mic decat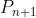 , la numarul
, la numarul ) se poate scoate factor comun un numar prim mai mic decat
se poate scoate factor comun un numar prim mai mic decat 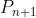 , deci nu este un numar prim.
, deci nu este un numar prim.
+P_{n+1}) este un numar care nu se divide cu niciun numar prim
este un numar care nu se divide cu niciun numar prim 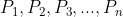 .
.
Deci toate numerele cuprinse intre+1) si
si +P_{n+1}) nu sunt prime .
nu sunt prime .
Asta nu inseamna ca numerele+1) si
si +P_{n+1}) sunt numere prime, ci doar ca exista
sunt numere prime, ci doar ca exista ![[(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+P_{n+1}] - [(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+1] =(P_{n+1}-1)](http://latex.codecogs.com/gif.latex?[(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+P_{n+1}] - [(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+1] =(P_{n+1}-1)) numere consecutive care nu sunt prime.
numere consecutive care nu sunt prime.
Deci putem sa scriem relatia :
![P_{x}\leq [(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+P_{n+1}] < [(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+1] \leq P_{x+1}](http://latex.codecogs.com/gif.latex?P_{x}\leq [(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+P_{n+1}] < [(P_{1}\cdot P_{2}\cdot P_{3}\cdot ...\cdot P_{n})+1] \leq P_{x+1}) ,
,
iar din cele scrise pana acum, rezulta ca exista doua numere prime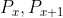 astfel incat
astfel incat 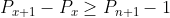 .
.
Pentru ca exista o infinitate de numere prime, inseamna ca exista un numar prim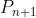 infinit de mare, sau mai corect, care tinde catre infinit, reprezentand diferenta minima dintre alte doua numere prime consecutive
infinit de mare, sau mai corect, care tinde catre infinit, reprezentand diferenta minima dintre alte doua numere prime consecutive 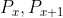 .
.
Deci aceasta "constanta"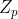 nu este un numar finit, ci tinde catre infinit.
nu este un numar finit, ci tinde catre infinit.
Bineinteles, in presupunerea ta:
"Pe de alta parte s-ar putea ca aceasta diferenta sa respecte inegalitatea p1>Cp>Zp unde Cp este o constanta a sirului
infinit de numere prime si mai afirm ca aceasta constanta Cp este un numar par.Cum am putea determina constanta Cp a sirului infinit de numere prime?",
atat timp cat limita minima a inegalitatii despre care vorbesti,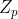 , tinde catre infinit, toate celelate limite trebuie obligatoriu sa tinda catre infinit pentru a fi adevarata relatia generala.
, tinde catre infinit, toate celelate limite trebuie obligatoriu sa tinda catre infinit pentru a fi adevarata relatia generala.
In concluzie, nu putem vorbi de constante finite.
Putem vorbi despre o constanta in densitatea numerelor prime in numere, si nu intre numerele prime,insa acesta este un aspect pe care il voi scrie intr-o lucrare completa pe care sper sa o termin anul acesta, intr-o ampla analiza a numerelor prime, ce contine si o parte din demonstratiile unor ipoteze privind numerele prime.
In primul rand, relatia p1>p2-p1 se demonstreaza prin Teorema Bertrand-Chebasev , in felul urmator:
(daca p1,p2 tu le consideri doua numere prime consecutive, atunci le voi rescrie la termenul general, adica
Prin aceasta teorema se demonstreaza ca intre x si 2x exista cel putin un numar prim.
Deci
Considerand x ca fiind numarul prim
In ceea ce priveste : "...ca desi aceasta diferenta Zp poate fi oricat de mare (zic unii)..."
Nu zic unii, ci mai degraba o demonstreaza "unii" in felul urmator :
etc.
Orice numar mai mic decat
Asta inseamna ca adunand oricare numar mai mare ca 1 si mai mic decat
Deci toate numerele cuprinse intre
Asta nu inseamna ca numerele
Deci putem sa scriem relatia :
iar din cele scrise pana acum, rezulta ca exista doua numere prime
Pentru ca exista o infinitate de numere prime, inseamna ca exista un numar prim
Deci aceasta "constanta"
Bineinteles, in presupunerea ta:
"Pe de alta parte s-ar putea ca aceasta diferenta sa respecte inegalitatea p1>Cp>Zp unde Cp este o constanta a sirului
infinit de numere prime si mai afirm ca aceasta constanta Cp este un numar par.Cum am putea determina constanta Cp a sirului infinit de numere prime?",
atat timp cat limita minima a inegalitatii despre care vorbesti,
In concluzie, nu putem vorbi de constante finite.
Putem vorbi despre o constanta in densitatea numerelor prime in numere, si nu intre numerele prime,insa acesta este un aspect pe care il voi scrie intr-o lucrare completa pe care sper sa o termin anul acesta, intr-o ampla analiza a numerelor prime, ce contine si o parte din demonstratiile unor ipoteze privind numerele prime.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Cred ca nu am fost bine inteles.Daca ne uitam cu atentie la sirul numerelor prime observam ca in sirul numerelor prime mai mari ca 2 si mai mici ca 10000 exista doar numerele prime p1=8467 si p2=8501 pentru care Zp=p2-p1=34 este cel mai mare.De cate ori este mai mare 8467 fata de Zp=34 se vede usor.Ma gandesc ca pe masura ce numerele prime sunt din ce in ce mai mari atunci cu atat mai mult pare plauzibila existenta constantei Cp a sirului infinit de numere prime si se mai observa ca in sirul numerelor prime pana la 10000 sunt foarte multe numere prime consecutive pentru care Zp este destul de mic cele mai multe fiind cu Zp=2,Zp=4 si Zp=6.Care este cel mai mare Zp din sirul numerelor prime pana la un miliard?Multumesc!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Ok.
Fi te rog, pentru inceput, ceva mai explicit pentru ca nu inteleg exact la ce raportezi constanta Cp.
Iar daca nu inteleg exact,nici nu pot sa-mi dau seama cum si ce ar trebui sa iti explic sau sa-mi spun parerea.
Pentru ca din mesajul/mesajele tale nu reiese exact.
Cp este cumva raportul p/Zp ?
Pentru ca asta reiese din :
"De cate ori este mai mare 8467 fata de Zp=34 se vede usor.Ma gandesc ca pe masura ce numerele prime sunt din ce in ce mai mari atunci cu atat mai mult pare plauzibila existenta constantei Cp a sirului infinit de numere prime"
In ceea ce priveste Zp, sa inteleg ca este cea mai mare diferenta dintre doua numere prime consecutive pana la un anumit numar m.
Daca este asa, si ca raspuns la :
"Care este cel mai mare Zp din sirul numerelor prime pana la un miliard? ",
iti raspund in felul urmator :
Daca P(n)
Poate daca imi spui la ce te ajuta si la ce iti foloseste, iti voi arata cum se demonstreaza asta.
Daca esti doar curios, atunci asteapta ceva timp si vei afla si cum se demonstreaza asta.
Dar daca vrei sa incerc sa-ti raspund sau sa-mi spun parerea, in masura in care sunt capabil, la intrebarile tale, trebuie sa stiu exact cum "vezi" aceste constante.
Deci, ce inseamna pentru tine Cp (si Zp) ?
Referitor la ceea ce ai spus :
"...si se mai observa ca in sirul numerelor prime pana la 10000 sunt foarte multe numere prime consecutive pentru care Zp este destul de mic cele mai multe fiind cu Zp=2,Zp=4 si Zp=6." ,
este ceea ce spuneam, adica o constanta raportata la numerele prime,
poate fi stabilita doar in ceea ce priveste densitatea lor, adica "locurile" in care sunt mai dese sau mai rare.
Voi vorbi la un moment dat si despre asta.
Astept sa-mi explici mai intai, Cp si Zp, astfel incat sa inteleg exact ce vrei sa spui si la ce te referi.
Fi te rog, pentru inceput, ceva mai explicit pentru ca nu inteleg exact la ce raportezi constanta Cp.
Iar daca nu inteleg exact,nici nu pot sa-mi dau seama cum si ce ar trebui sa iti explic sau sa-mi spun parerea.
Pentru ca din mesajul/mesajele tale nu reiese exact.
Cp este cumva raportul p/Zp ?
Pentru ca asta reiese din :
"De cate ori este mai mare 8467 fata de Zp=34 se vede usor.Ma gandesc ca pe masura ce numerele prime sunt din ce in ce mai mari atunci cu atat mai mult pare plauzibila existenta constantei Cp a sirului infinit de numere prime"
In ceea ce priveste Zp, sa inteleg ca este cea mai mare diferenta dintre doua numere prime consecutive pana la un anumit numar m.
Daca este asa, si ca raspuns la :
"Care este cel mai mare Zp din sirul numerelor prime pana la un miliard? ",
iti raspund in felul urmator :
Daca P(n)
Poate daca imi spui la ce te ajuta si la ce iti foloseste, iti voi arata cum se demonstreaza asta.
Daca esti doar curios, atunci asteapta ceva timp si vei afla si cum se demonstreaza asta.
Dar daca vrei sa incerc sa-ti raspund sau sa-mi spun parerea, in masura in care sunt capabil, la intrebarile tale, trebuie sa stiu exact cum "vezi" aceste constante.
Deci, ce inseamna pentru tine Cp (si Zp) ?
Referitor la ceea ce ai spus :
"...si se mai observa ca in sirul numerelor prime pana la 10000 sunt foarte multe numere prime consecutive pentru care Zp este destul de mic cele mai multe fiind cu Zp=2,Zp=4 si Zp=6." ,
este ceea ce spuneam, adica o constanta raportata la numerele prime,
poate fi stabilita doar in ceea ce priveste densitatea lor, adica "locurile" in care sunt mai dese sau mai rare.
Voi vorbi la un moment dat si despre asta.
Astept sa-mi explici mai intai, Cp si Zp, astfel incat sa inteleg exact ce vrei sa spui si la ce te referi.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Se pare ca folosind caracterele < si > se anuleaza o parte din text, recunoscandu-l ca un cod html.
In mesajul meu anterior a fost eliminat o parte din text, din aceste motive.
In mesajul meu anterior a fost eliminat o parte din text, din aceste motive.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Din motivele mentionate in mesajul anterior, am rescris mesajul incadrand semnele < si > intre doua virgule sa vad daca sunt afisate.
Ok.
Fi te rog, pentru inceput, ceva mai explicit pentru ca nu inteleg exact la ce raportezi constanta Cp.
Iar daca nu inteleg exact,nici nu pot sa-mi dau seama cum si ce ar trebui sa iti explic sau sa-mi spun parerea.
Pentru ca din mesajul/mesajele tale nu reiese exact.
Cp este cumva raportul p/Zp ?
Pentru ca asta reiese din :
"De cate ori este mai mare 8467 fata de Zp=34 se vede usor.Ma gandesc ca pe masura ce numerele prime sunt din ce in ce mai mari atunci cu atat mai mult pare plauzibila existenta constantei Cp a sirului infinit de numere prime"
In ceea ce priveste Zp, sa inteleg ca este cea mai mare diferenta dintre doua numere prime consecutive pana la un anumit numar n.
Daca este asa, si ca raspuns la :
"Care este cel mai mare Zp din sirul numerelor prime pana la un miliard? ", iti raspund in felul urmator :
Daca P(n),<,sqrt(un miliard),<,P(n+1), cea mai mare diferenta dintre doua numere prime consecutive pana la un miliard este cel mult 2[P(n-1)].
Verifica, daca vrei sa te convingi, pentru orice numar m, nu neaparat un miliard. Conditia de care trebuie sa tii cont este P(n),<, sqrt(m),<,P(n+1) si pana la acel m, diferenta cea mai mare dintre doua numere prime consecutive este cel mult 2P(n-1).
Nu am timp acum sa-ti demonstrez cum rezulta asta si sa scriu in LaTex.
Poate daca imi spui la ce te ajuta si la ce iti foloseste, iti voi arata cum se demonstreaza asta.
Daca esti doar curios, atunci asteapta ceva timp si vei afla si cum se demonstreaza asta.
Dar daca vrei sa incerc sa-ti raspund sau sa-mi spun parerea, in masura in care sunt capabil, la intrebarile tale, trebuie sa stiu exact cum "vezi" aceste constante.
Deci, ce inseamna pentru tine Cp (si Zp) ?
Referitor la ceea ce ai spus :
"...si se mai observa ca in sirul numerelor prime pana la 10000 sunt foarte multe numere prime consecutive pentru care Zp este destul de mic cele mai multe fiind cu Zp=2,Zp=4 si Zp=6." ,
este ceea ce spuneam, adica o constanta raportata la numerele prime,
poate fi stabilita doar in ceea ce priveste densitatea lor, adica "locurile" in care sunt mai dese sau mai rare.
Voi vorbi la un moment dat si despre asta.
Astept sa-mi explici mai intai, Cp si Zp, astfel incat sa inteleg exact ce vrei sa spui si la ce te referi.
Ok.
Fi te rog, pentru inceput, ceva mai explicit pentru ca nu inteleg exact la ce raportezi constanta Cp.
Iar daca nu inteleg exact,nici nu pot sa-mi dau seama cum si ce ar trebui sa iti explic sau sa-mi spun parerea.
Pentru ca din mesajul/mesajele tale nu reiese exact.
Cp este cumva raportul p/Zp ?
Pentru ca asta reiese din :
"De cate ori este mai mare 8467 fata de Zp=34 se vede usor.Ma gandesc ca pe masura ce numerele prime sunt din ce in ce mai mari atunci cu atat mai mult pare plauzibila existenta constantei Cp a sirului infinit de numere prime"
In ceea ce priveste Zp, sa inteleg ca este cea mai mare diferenta dintre doua numere prime consecutive pana la un anumit numar n.
Daca este asa, si ca raspuns la :
"Care este cel mai mare Zp din sirul numerelor prime pana la un miliard? ", iti raspund in felul urmator :
Daca P(n),<,sqrt(un miliard),<,P(n+1), cea mai mare diferenta dintre doua numere prime consecutive pana la un miliard este cel mult 2[P(n-1)].
Verifica, daca vrei sa te convingi, pentru orice numar m, nu neaparat un miliard. Conditia de care trebuie sa tii cont este P(n),<, sqrt(m),<,P(n+1) si pana la acel m, diferenta cea mai mare dintre doua numere prime consecutive este cel mult 2P(n-1).
Nu am timp acum sa-ti demonstrez cum rezulta asta si sa scriu in LaTex.
Poate daca imi spui la ce te ajuta si la ce iti foloseste, iti voi arata cum se demonstreaza asta.
Daca esti doar curios, atunci asteapta ceva timp si vei afla si cum se demonstreaza asta.
Dar daca vrei sa incerc sa-ti raspund sau sa-mi spun parerea, in masura in care sunt capabil, la intrebarile tale, trebuie sa stiu exact cum "vezi" aceste constante.
Deci, ce inseamna pentru tine Cp (si Zp) ?
Referitor la ceea ce ai spus :
"...si se mai observa ca in sirul numerelor prime pana la 10000 sunt foarte multe numere prime consecutive pentru care Zp este destul de mic cele mai multe fiind cu Zp=2,Zp=4 si Zp=6." ,
este ceea ce spuneam, adica o constanta raportata la numerele prime,
poate fi stabilita doar in ceea ce priveste densitatea lor, adica "locurile" in care sunt mai dese sau mai rare.
Voi vorbi la un moment dat si despre asta.
Astept sa-mi explici mai intai, Cp si Zp, astfel incat sa inteleg exact ce vrei sa spui si la ce te referi.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Studiez acum numerele prime de forma  unde
unde  este un numar natural oarecare iar
este un numar natural oarecare iar  este un numar intreg oarecare.De exemplu intre numerele
este un numar intreg oarecare.De exemplu intre numerele  si
si  exista 6 numere prime iar intre numerele
exista 6 numere prime iar intre numerele  si
si  exista 7 numere prime.Se stie ca intre numerele
exista 7 numere prime.Se stie ca intre numerele  si
si  pot exista cel mult 40 de numere prime.Ma gandesc sa aflu care este numarul minim de numere prime existente intre numerele
pot exista cel mult 40 de numere prime.Ma gandesc sa aflu care este numarul minim de numere prime existente intre numerele  si
si  .Dupa care voi analiza si acel
.Dupa care voi analiza si acel  din cadrul acestor intervale de numere.
din cadrul acestor intervale de numere.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
In primul rand te felicit pentru aceasta preocupare.
Numerele prime sunt un pic mai speciale datorita iregularitatii distributiei lor.
Eu o sa-ti raspund mereu la mesajele tale, in speranta ca informatiile mele iti pot fi folositoare si te vor ajuta sa nu pierzi timp degeaba in analiza unor aspecte care nu au marre insemnatate sau valoare de adevar.
Deci,
ai afirmat:
"Se stie ca intre numerele 10^k si 10^k+10^2 pot exista cel mult 40 de numere prime "
Fie ai gresit puterea 2 de la 10^2, fie observatia ta este falsa.
Singurul interval de numere consecutive egal cu 10^2 in care exista cel mai mare numar de numere prime, este intre 10^0 si 10^0 +10^2,adica intre 1 si 100.
In acest interval sunt doar 25 de numere prime si nu exista un alt interval de 100 de numere naturale consecutive in care sa fie mai mult de 25 de numere prime, pentru simplul motiv ca ele se raresc.
Verifica.
Afirmatia mea este bazata doar pe experienta mea cu aceste numere, fara sa calculez sau sa verific personal daca am dreptate sau nu,sunt sigur ca nu vei gasi un alt interval de 100 de numere in caresa existe mai mult de 25 de numere prime, nicidecum 40.
As putea sa-ti dezvolt si un rationament din care reiese asta.
Referitor la :
"Ma gandesc sa aflu care este numarul minim de numere prime existente intre numerele 10^k si 10^k+10^2.",
la nivelul unor numere prime extrem de mari, diferenta dintre ele este suficient de mare ca intr-un interval de 100 (10^2) numere consecutive sa nu existe niciun numar prim.
Fara sa te superi,
observ ca ai adus de multe ori in vedere numerele prime pana la o putere de 10.
Aceste valori sunt pur orientative raportate la numerele prime, pentru a forma o idee de ansamblu referitoare la modul in care ele se raresc si nu vorbesc exact despre numarul lor.
Tu poti sa continui sa calculezi ce vrei si cum vrei.
Eu sper sa intelegi doar ca in spatele parerilor mele din acest subiect, stau ani de calcul si analiza a numerele prime, motiv pentru care sper sa-ti fie folositoare.
Numerele prime sunt un pic mai speciale datorita iregularitatii distributiei lor.
Eu o sa-ti raspund mereu la mesajele tale, in speranta ca informatiile mele iti pot fi folositoare si te vor ajuta sa nu pierzi timp degeaba in analiza unor aspecte care nu au marre insemnatate sau valoare de adevar.
Deci,
ai afirmat:
"Se stie ca intre numerele 10^k si 10^k+10^2 pot exista cel mult 40 de numere prime "
Fie ai gresit puterea 2 de la 10^2, fie observatia ta este falsa.
Singurul interval de numere consecutive egal cu 10^2 in care exista cel mai mare numar de numere prime, este intre 10^0 si 10^0 +10^2,adica intre 1 si 100.
In acest interval sunt doar 25 de numere prime si nu exista un alt interval de 100 de numere naturale consecutive in care sa fie mai mult de 25 de numere prime, pentru simplul motiv ca ele se raresc.
Verifica.
Afirmatia mea este bazata doar pe experienta mea cu aceste numere, fara sa calculez sau sa verific personal daca am dreptate sau nu,sunt sigur ca nu vei gasi un alt interval de 100 de numere in caresa existe mai mult de 25 de numere prime, nicidecum 40.
As putea sa-ti dezvolt si un rationament din care reiese asta.
Referitor la :
"Ma gandesc sa aflu care este numarul minim de numere prime existente intre numerele 10^k si 10^k+10^2.",
la nivelul unor numere prime extrem de mari, diferenta dintre ele este suficient de mare ca intr-un interval de 100 (10^2) numere consecutive sa nu existe niciun numar prim.
Fara sa te superi,
observ ca ai adus de multe ori in vedere numerele prime pana la o putere de 10.
Aceste valori sunt pur orientative raportate la numerele prime, pentru a forma o idee de ansamblu referitoare la modul in care ele se raresc si nu vorbesc exact despre numarul lor.
Tu poti sa continui sa calculezi ce vrei si cum vrei.
Eu sper sa intelegi doar ca in spatele parerilor mele din acest subiect, stau ani de calcul si analiza a numerele prime, motiv pentru care sper sa-ti fie folositoare.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
OK, intrebarea a fost serioasa si a avut un anumit talc .
Insa acum, nu mai am ce discuta ....
Nu vei sti niciodata de ce am pus aceasta intrebare .
Insa acum, nu mai am ce discuta ....
Nu vei sti niciodata de ce am pus aceasta intrebare .
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Cadi,
in primul rand nu eu am vopsit cu rosu penultimul tau mesaj.
Si afirm asta pentru ca ultimul tau mesaj este direct legat de modul in care ai interpretat rosul din penultimul mesaj.
Talcul despre care vorbesti nu-mi este de folos daca nu inteleg nimic din el.
Iti dau un sfat si nu te grabi sa-mi raspunzi.
Tu esti baiat istet, dar se pare ca ti-ai deformat un pic sistemul de valori referitor la activitatea ta pe forum.
Parerea mea, gresita sau nu, este ca te-ai obisnuit gresit sa faci din acest forum un loc in care esti cel mai apreciat si esti in varful unor anumite sondaje si nu sa intelegi ceva, sa te dezvoltila nivel personal.
Cu stima.
Daca raspunsul tau vine ca o replica la acest mesaj imi confirmi adevarul spuselor mele.
in primul rand nu eu am vopsit cu rosu penultimul tau mesaj.
Si afirm asta pentru ca ultimul tau mesaj este direct legat de modul in care ai interpretat rosul din penultimul mesaj.
Talcul despre care vorbesti nu-mi este de folos daca nu inteleg nimic din el.
Iti dau un sfat si nu te grabi sa-mi raspunzi.
Tu esti baiat istet, dar se pare ca ti-ai deformat un pic sistemul de valori referitor la activitatea ta pe forum.
Parerea mea, gresita sau nu, este ca te-ai obisnuit gresit sa faci din acest forum un loc in care esti cel mai apreciat si esti in varful unor anumite sondaje si nu sa intelegi ceva, sa te dezvoltila nivel personal.
Cu stima.
Daca raspunsul tau vine ca o replica la acest mesaj imi confirmi adevarul spuselor mele.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
La asemenea acuzatii nici nu stiu ce sa raspund!
A fost o simpla intrebare ! Pe cine l-a deranjat atat de mult ?
Se pare ca unii nu se gandesc decat la faptul ce reprezinta ei in ochii altora si la punctajul lor de pe forum... Iar anumite subiecte in care ei cred cu tarie ,pentru ei sunt tabu !Nu vor sa mearga mai departe si sa asculte si alte idei...
Punctajul nu reprezinta nimic in ochii mei (poate doar in ochii altora
care alearga dupa asa ceva).
Iar forumul este un loc in care se schimba pareri si idei si un loc din care invatam foarte mult unii de la altii...Nu este un loc de confruntari.
Se pare insa ca pentru unii , reprezinta mult mai mult ...
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Nu am gresit nimic referitor la afirmatia mea deoarece tocmai pentru ca nu exista o regularitate de existenta a numerelor prime rezulta ca exista posibilitatea ca intre numerelecuriosul a scris:In primul rand te felicit pentru aceasta preocupare.
Numerele prime sunt un pic mai speciale datorita iregularitatii distributiei lor.
Eu o sa-ti raspund mereu la mesajele tale, in speranta ca informatiile mele iti pot fi folositoare si te vor ajuta sa nu pierzi timp degeaba in analiza unor aspecte care nu au marre insemnatate sau valoare de adevar.
Deci,
ai afirmat:
"Se stie ca intre numerele 10^k si 10^k+10^2 pot exista cel mult 40 de numere prime "
Fie ai gresit puterea 2 de la 10^2, fie observatia ta este falsa.
Singurul interval de numere consecutive egal cu 10^2 in care exista cel mai mare numar de numere prime, este intre 10^0 si 10^0 +10^2,adica intre 1 si 100.
In acest interval sunt doar 25 de numere prime si nu exista un alt interval de 100 de numere naturale consecutive in care sa fie mai mult de 25 de numere prime, pentru simplul motiv ca ele se raresc.
Verifica.
Afirmatia mea este bazata doar pe experienta mea cu aceste numere, fara sa calculez sau sa verific personal daca am dreptate sau nu,sunt sigur ca nu vei gasi un alt interval de 100 de numere in caresa existe mai mult de 25 de numere prime, nicidecum 40.
As putea sa-ti dezvolt si un rationament din care reiese asta.
Referitor la :
"Ma gandesc sa aflu care este numarul minim de numere prime existente intre numerele 10^k si 10^k+10^2.",
la nivelul unor numere prime extrem de mari, diferenta dintre ele este suficient de mare ca intr-un interval de 100 (10^2) numere consecutive sa nu existe niciun numar prim.
Fara sa te superi,
observ ca ai adus de multe ori in vedere numerele prime pana la o putere de 10.
Aceste valori sunt pur orientative raportate la numerele prime, pentru a forma o idee de ansamblu referitoare la modul in care ele se raresc si nu vorbesc exact despre numarul lor.
Tu poti sa continui sa calculezi ce vrei si cum vrei.
Eu sper sa intelegi doar ca in spatele parerilor mele din acest subiect, stau ani de calcul si analiza a numerele prime, motiv pentru care sper sa-ti fie folositoare.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Nu trebuie sa-ti demonstreze nimeni.
Poti sa-ti demonstrezi singur.
Eu o sa-ti arat o modalitate usoara prin care sa verifici asta.
Deci intre 1 si 100 sunt 25 de numere prime.
In acest interval, orice numar care nu este prim, se divide cu cel putin unul din numerele prime 2,3,5,7, pentru ca cel mai mare numar prim pana la radical din 100 este 7.
In continuare, consideri fiind un numar prim, orice numar care nu se divide cu 2,3,5 sau 7.
Aceste numere le gasesti cu usurinta cunoscand doar numerele care nu se divid cu 2,3,5 sau 7, pana la numarul 210 (2*3*5*7).
Pentru ca daca m este un numar care nu se divide cu 2,3,5 sau 7, atunci nici 210+m nu se divide cu aceste numere prime.
In acest moment iti ramane sa calculezi (sa verifici) doar daca in oricare interval [x, x+100], pentru x<210, pot exista mai mult de 25 de numere care nu se divid doar cu 2,3,5 sau 7.
Iti ia cel mult 10 minute fara bataie de cap.
Incearca sa gandesti si singur de ce functioneaza aceasta modalitate.
Simpla si eficienta.
Poti sa-ti demonstrezi singur.
Eu o sa-ti arat o modalitate usoara prin care sa verifici asta.
Deci intre 1 si 100 sunt 25 de numere prime.
In acest interval, orice numar care nu este prim, se divide cu cel putin unul din numerele prime 2,3,5,7, pentru ca cel mai mare numar prim pana la radical din 100 este 7.
In continuare, consideri fiind un numar prim, orice numar care nu se divide cu 2,3,5 sau 7.
Aceste numere le gasesti cu usurinta cunoscand doar numerele care nu se divid cu 2,3,5 sau 7, pana la numarul 210 (2*3*5*7).
Pentru ca daca m este un numar care nu se divide cu 2,3,5 sau 7, atunci nici 210+m nu se divide cu aceste numere prime.
In acest moment iti ramane sa calculezi (sa verifici) doar daca in oricare interval [x, x+100], pentru x<210, pot exista mai mult de 25 de numere care nu se divid doar cu 2,3,5 sau 7.
Iti ia cel mult 10 minute fara bataie de cap.
Incearca sa gandesti si singur de ce functioneaza aceasta modalitate.
Simpla si eficienta.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Si tu esti baiat istet curiosu, ai priceput ideea .... 
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Fara suparare!Ma tem ca nu se intelege ce am spus eu.Sa inteleg ca afirmatia "daca m este un numar care nu se divide cu 2,3,5 sau 7, atunci nici 210+m nu se divide cu aceste numere prime" atunci numarul 210+m este numar prim?curiosul a scris:Nu trebuie sa-ti demonstreze nimeni.
Poti sa-ti demonstrezi singur.
Eu o sa-ti arat o modalitate usoara prin care sa verifici asta.
Deci intre 1 si 100 sunt 25 de numere prime.
In acest interval, orice numar care nu este prim, se divide cu cel putin unul din numerele prime 2,3,5,7, pentru ca cel mai mare numar prim pana la radical din 100 este 7.
In continuare, consideri fiind un numar prim, orice numar care nu se divide cu 2,3,5 sau 7.
Aceste numere le gasesti cu usurinta cunoscand doar numerele care nu se divid cu 2,3,5 sau 7, pana la numarul 210 (2*3*5*7).
Pentru ca daca m este un numar care nu se divide cu 2,3,5 sau 7, atunci nici 210+m nu se divide cu aceste numere prime.
In acest moment iti ramane sa calculezi (sa verifici) doar daca in oricare interval [x, x+100], pentru x<210, pot exista mai mult de 25 de numere care nu se divid doar cu 2,3,5 sau 7.
Iti ia cel mult 10 minute fara bataie de cap.
Incearca sa gandesti si singur de ce functioneaza aceasta modalitate.
Simpla si eficienta.
Nu inteleg de ce se limiteaza valoarea lui x la maxim valoarea lui 210 asa cum reiese din afirmatia "In acest moment iti ramane sa calculezi (sa verifici) doar daca in oricare interval [x, x+100], pentru x<210, pot exista mai mult de 25 de numere care nu se divid doar cu 2,3,5 sau 7."?
Eu am afirmat ca pentru anumite numere naturale
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Sigur, iti raspund cu placere.
Dar trebuie sa faci un "efort" practic sa intelegi ce-ti spun.
Adica sa pui creionul pe hartie sa-ti dai singur seama de ceea ce spun.
1. In primul rand, daca ne referim la orice interval de 100 de numere naturale consecutive, indirect se subantelege si oricare interval
[10^k, 10^k+10^2]. Pentru ca acest interval este inclus in "orice interval", asa cum am afirmat mai sus.
2. Daca intr-un anumit interval de 100 de numere naturale consecutive, sunt, sa spunem, cel mult 25 de numere care nu se divid cu 2,3,5 sau 7, asta inseamna ca in acel interval sunt si cel mult 25 de numere prime.
Pentru ca numarul acestor numere prime din acel interval, este inclus in numerele care nu se divid cu 2,3,5 sau 7, ceea ce inseamna ca daca sunt cel mult 25 de numere naturale care nu se divid cu 2,3,5, sau 7, inseamna ca sunt si cel mult 25 de numere prime. Este totusi posibil, ca intre numerele care nu se divid cu 2,3,5 sau7, sa mai existe numere care se divid cu 11,13,17,..., deci care nu sunt prime.
Insa logica afirmatiei se pastreaza. Numarul de numere prime din acel interval este cel mult numarul de numere naturale care nu se divid cu 2,3,5 sau 7. Cazul intervalului [1, 100], interval in care toate numerele care nu se divid cu 2,3,5 sau 7 sunt toate numere prime.
3. Iti este suficient cel mult doua pagini de hartie si un milimetru de mina de creion sau 5 minute de "vizualizare" a situatiei, sa-ti dai seama ca numerele naturale care nu se divid cu 2,3,5 sau 7, se gasesc distribuite in numere cu o periodicitate egala cu 210 (adica 2*3*5*7).
Exceptia de la regula, se regaseste doar in intervalul [1, 100], pentru ca numerele 2,3,5 si 7 din intervalul de mai sus apar ca numere prime si nu ca factori primi. Adica pentru m=7, atunci 210+7 se divide cu 7. Deci cu exceptia numerelor 2,3,5 si 7 si a numarului 1, care trebuie considerat prim, toate numerele care nu se divid cu 2,3,5 si 7 se regasesc dupa o constanta, dupa o periodicitate de 210.
4. Din 3. rezulta ca numarul de numere naturale consecutive care nu se divid cu 2, 3, 5 si 7 din intervalul [x, x+100] este identic cu numarul de numere naturale care nu se divid cu 2, 3, 5 si 7 din orice interval [ (x+210k), (x+210K+100) ].
5. In consecinta, este suficient sa cunosti intervalul in care exista cel mai mare numar de numere naturale consecutive [x, x+100] , pentru orice x<210. Pentru ca din 4. rezulta ca acel numar este cel mai mare numar de numere naturale consecutive care nu se divid cu 2, 3, 5 si 7, regasindu-se cu o periodicitate de 210, cum rezulta din 4.
6. Daca faci un efort si calculezi ce ti-am spus, vei ajunge singur la concluzia ca in orice interval de 100 numere naturale consecutive, poate exista cel mult...(concluzia la care ajungi tu)
Nu ma supar de loc si iti explic cu multa placere.
Insa trebuie sa verifici si practic ceea ce iti spun, pentru ca daca iti dezvolt rationamente mai complicate, prin expresii matematice, nu le intelegi daca nu verifici practic, adica sa calculezi un pic si singur.
Matematica se invata cu creionul pe hartie, nu citind din carti.
Afirmatia de mai sus nu este o aluzie adresata tie sau altora.
Asta este doar concluzia la care am ajuns eu.
Cu stima si te astept sa-mi spui la ce concluzie ai ajuns.
Dar trebuie sa faci un "efort" practic sa intelegi ce-ti spun.
Adica sa pui creionul pe hartie sa-ti dai singur seama de ceea ce spun.
1. In primul rand, daca ne referim la orice interval de 100 de numere naturale consecutive, indirect se subantelege si oricare interval
[10^k, 10^k+10^2]. Pentru ca acest interval este inclus in "orice interval", asa cum am afirmat mai sus.
2. Daca intr-un anumit interval de 100 de numere naturale consecutive, sunt, sa spunem, cel mult 25 de numere care nu se divid cu 2,3,5 sau 7, asta inseamna ca in acel interval sunt si cel mult 25 de numere prime.
Pentru ca numarul acestor numere prime din acel interval, este inclus in numerele care nu se divid cu 2,3,5 sau 7, ceea ce inseamna ca daca sunt cel mult 25 de numere naturale care nu se divid cu 2,3,5, sau 7, inseamna ca sunt si cel mult 25 de numere prime. Este totusi posibil, ca intre numerele care nu se divid cu 2,3,5 sau7, sa mai existe numere care se divid cu 11,13,17,..., deci care nu sunt prime.
Insa logica afirmatiei se pastreaza. Numarul de numere prime din acel interval este cel mult numarul de numere naturale care nu se divid cu 2,3,5 sau 7. Cazul intervalului [1, 100], interval in care toate numerele care nu se divid cu 2,3,5 sau 7 sunt toate numere prime.
3. Iti este suficient cel mult doua pagini de hartie si un milimetru de mina de creion sau 5 minute de "vizualizare" a situatiei, sa-ti dai seama ca numerele naturale care nu se divid cu 2,3,5 sau 7, se gasesc distribuite in numere cu o periodicitate egala cu 210 (adica 2*3*5*7).
Exceptia de la regula, se regaseste doar in intervalul [1, 100], pentru ca numerele 2,3,5 si 7 din intervalul de mai sus apar ca numere prime si nu ca factori primi. Adica pentru m=7, atunci 210+7 se divide cu 7. Deci cu exceptia numerelor 2,3,5 si 7 si a numarului 1, care trebuie considerat prim, toate numerele care nu se divid cu 2,3,5 si 7 se regasesc dupa o constanta, dupa o periodicitate de 210.
4. Din 3. rezulta ca numarul de numere naturale consecutive care nu se divid cu 2, 3, 5 si 7 din intervalul [x, x+100] este identic cu numarul de numere naturale care nu se divid cu 2, 3, 5 si 7 din orice interval [ (x+210k), (x+210K+100) ].
5. In consecinta, este suficient sa cunosti intervalul in care exista cel mai mare numar de numere naturale consecutive [x, x+100] , pentru orice x<210. Pentru ca din 4. rezulta ca acel numar este cel mai mare numar de numere naturale consecutive care nu se divid cu 2, 3, 5 si 7, regasindu-se cu o periodicitate de 210, cum rezulta din 4.
6. Daca faci un efort si calculezi ce ti-am spus, vei ajunge singur la concluzia ca in orice interval de 100 numere naturale consecutive, poate exista cel mult...(concluzia la care ajungi tu)
Nu ma supar de loc si iti explic cu multa placere.
Insa trebuie sa verifici si practic ceea ce iti spun, pentru ca daca iti dezvolt rationamente mai complicate, prin expresii matematice, nu le intelegi daca nu verifici practic, adica sa calculezi un pic si singur.
Matematica se invata cu creionul pe hartie, nu citind din carti.
Afirmatia de mai sus nu este o aluzie adresata tie sau altora.
Asta este doar concluzia la care am ajuns eu.
Cu stima si te astept sa-mi spui la ce concluzie ai ajuns.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Sa inteleg ca in sirul oricarei sute de numere naturale consecutive se pot afla cel mult 25 numere prime?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Pai separe ca nu, exemplu intervalului [2, 102] unde sunt 26 de numere prime, deci mai mare decat 25.
Nu pentru mine este important care este numarul maxim de numere prime dintr-o suta de numere naturale consecutive, ci pentru tine.
Eu vreau sa te ajut sa afli care este acest numar maxim de numere prime.
Sper sa intelegi asta.
Nu pentru mine este important care este numarul maxim de numere prime dintr-o suta de numere naturale consecutive, ci pentru tine.
Eu vreau sa te ajut sa afli care este acest numar maxim de numere prime.
Sper sa intelegi asta.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Mai mult, as numi numarul 1- numarul prim absolut.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Problema numerelor prime
Re: Problema numerelor prime
Eu as numi numarul 1 singurul numar prim !
Celelate numere prime sunt avatari ai numarului prim absolut 1 .
Celelate numere prime sunt avatari ai numarului prim absolut 1 .
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Conjectura:
Exista o infinitate de numere naturale si de numere intregi
si de numere intregi  astfel incat intre numerele
astfel incat intre numerele  si
si  exista
exista  de numere prime.
de numere prime.
Exista o infinitate de numere naturale
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Rectific mesajul anterior.
Conjectura:
Exista o infinitate de numere naturale astfel incat intre numerele
astfel incat intre numerele  si
si  exista
exista  de numere prime.
de numere prime.
Conjectura:
Exista o infinitate de numere naturale
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Problema numerelor prime
Re: Problema numerelor prime
Dacu,
tiparul tau logic de insiruire a ideilor intr-un subiect, precum si logica prin care intervii intr-un subiect, este identica cu a unui utilizator de pe acest forum, AMOT.
Inainte sa conjecturezi ceva matematic, mi se pare logic sa tii cont de toate informatiile despre conjectura ta, deci implicit ceea ce am spus eu.
Te hazardezi sa conjecturezi ceva raportat la numerele prime, fara sa ai o ampla anailza initiala despre numerele prime.
Eu iti dorec mult succes si pentru simplul fapt ca ti-e lene sa analizezi ce spun, conjecturezi ceva fara a avea o mare implicatie in studiul numerelor prime, inclin sa cred ca parerile mele sunt zero pentru tine, deci nu mai meriti sa-mi spun parerea la nedumeririle tale din acest subiect.
Prudent ar fi fost sa-mi explici mai intai de ce ma insel, inainte sa conjecturezi ceva.
O sa mai astept pana gasesc pe cineva interesat de analizele mele si de experienta mea cu numerele prime.
Cu prietenie,
curiosul
tiparul tau logic de insiruire a ideilor intr-un subiect, precum si logica prin care intervii intr-un subiect, este identica cu a unui utilizator de pe acest forum, AMOT.
Inainte sa conjecturezi ceva matematic, mi se pare logic sa tii cont de toate informatiile despre conjectura ta, deci implicit ceea ce am spus eu.
Te hazardezi sa conjecturezi ceva raportat la numerele prime, fara sa ai o ampla anailza initiala despre numerele prime.
Eu iti dorec mult succes si pentru simplul fapt ca ti-e lene sa analizezi ce spun, conjecturezi ceva fara a avea o mare implicatie in studiul numerelor prime, inclin sa cred ca parerile mele sunt zero pentru tine, deci nu mai meriti sa-mi spun parerea la nedumeririle tale din acest subiect.
Prudent ar fi fost sa-mi explici mai intai de ce ma insel, inainte sa conjecturezi ceva.
O sa mai astept pana gasesc pe cineva interesat de analizele mele si de experienta mea cu numerele prime.
Cu prietenie,
curiosul
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
Pagina 2 din 4 •  1, 2, 3, 4
1, 2, 3, 4 
Pagina 2 din 4
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
