Problema numerelor prime

Scris de **Abel Cavaşi** Mier 12 Mar 2008, 21:08

Rezumarea primului mesaj :

Încă din adolescenţă am fost captivat de problema numerelor prime. Cineva mi-a spus că încă nu se cunoaşte cum sunt ordonate numerele prime, iar eu nu am vrut să-l cred că problema este chiar atât de complicată. Se pare că, totuşi, e. Shocked

Mai exact, fie dat şirul numerelor prime

n	1	2	3	4	5	6	7	8	9	...
p	2	3	5	7	11	13	17	19	23	...

Se pune problema de a stabili o legătură directă între numărul n şi numărul p. Cu alte cuvinte, dându-se numărul n, oricare ar fi acesta, să se determine al n-lea număr prim din şirul infinit al numerelor prime.
Cine va rezolva această problemă ne va da o formulă minunată care ne va permite să obţinem, de exemplu, din 7, 17 sau din 9, 23, etc.

Cândva, pe vremea când aveam mai mult timp liber, am găsit o soluţie la problema inversă: dându-se numărul prim p, să se găsească al câtelea număr prim este el în şirul numerelor prime. Dacă o voi găsi printre hârtiile mele vechi, o voi posta aici. Ştiu că era ceva cu partea întreagă a unui număr.

Vă doresc succes tuturor celor care se încumetă!

Scris de **Dacu** Lun 10 Sept 2012, 12:46

Rectific mesajul anterior.
Conjectura:
Exista o infinitate de numere naturale $Problema numerelor prime - Pagina 3 Mimetex$ astfel incat intre numerele $Problema numerelor prime - Pagina 3 Mimetex$ si $Problema numerelor prime - Pagina 3 Mimetex$ exista $Problema numerelor prime - Pagina 3 Mimetex$ de numere prime.

Scris de **curiosul** Lun 10 Sept 2012, 12:55

Dacu,
tiparul tau logic de insiruire a ideilor intr-un subiect, precum si logica prin care intervii intr-un subiect, este identica cu a unui utilizator de pe acest forum, AMOT.

Inainte sa conjecturezi ceva matematic, mi se pare logic sa tii cont de toate informatiile despre conjectura ta, deci implicit ceea ce am spus eu.
Te hazardezi sa conjecturezi ceva raportat la numerele prime, fara sa ai o ampla anailza initiala despre numerele prime.
Eu iti dorec mult succes si pentru simplul fapt ca ti-e lene sa analizezi ce spun, conjecturezi ceva fara a avea o mare implicatie in studiul numerelor prime, inclin sa cred ca parerile mele sunt zero pentru tine, deci nu mai meriti sa-mi spun parerea la nedumeririle tale din acest subiect.
Prudent ar fi fost sa-mi explici mai intai de ce ma insel, inainte sa conjecturezi ceva.
O sa mai astept pana gasesc pe cineva interesat de analizele mele si de experienta mea cu numerele prime.
Cu prietenie,
curiosul

Scris de **Dacu** Lun 10 Sept 2012, 13:18

Fara suparare!Cine se aseamana se aduna!Asa ca Amot fiind amicul meu nu vad de ce nu am avea de multe ori aceleasi rationamente.
Cu Amot discut uneori despre numerele prime si de multe ori avem aceiasi parere dar eu am dat aceasta conjectura deoarece sunt sigur ca exista constanta sirului de numere prime $Problema numerelor prime - Pagina 3 Mimetex$ astfel incat $Problema numerelor prime - Pagina 3 Mimetex$ unde $Problema numerelor prime - Pagina 3 Mimetex$ sunt doua numere prime consecutive oarecare astfel incat $Problema numerelor prime - Pagina 3 Mimetex$ .Daca e cineva care va vrea sa-mi raspunda atunci eu voi fi pe faza si voi analiza ceea ce spune.Lasa-l in pace pe Amot si mai bine ar fi daca s-ar putea gasi vreo demonstratie care sa infirme conjectura mea.Vad ca acum sunt 26 de numere prime in sirul marginit de numerele 2 si 102 si nu vad de ce nu s-ar gasi un sir de o suta de numere naturale consecutive astfel incat in acest sir sa existe 40 de numere prime.

Scris de **curiosul** Lun 10 Sept 2012, 14:11

Va doresc mult suucces.
Transmite-i amicului tau Amot ca niciodata nu l-am subestimat.
Cu stima amandurora, curiosul.

Scris de **Abel Cavaşi** Lun 10 Sept 2012, 14:23

Aşa cum am promis la începutul acestui topic:

La începutul acestui topic, Abel Cavaşi a scris:Cândva, pe vremea când aveam mai mult timp liber, am găsit o soluţie la problema inversă: dându-se numărul prim p, să se găsească al câtelea număr prim este el în şirul numerelor prime. Dacă o voi găsi printre hârtiile mele vechi, o voi posta aici. Ştiu că era ceva cu partea întreagă a unui număr.

,
postez aici ceea ce am scris şi pe blogul meu prin 2011:

Pe blogul său, Abel Cavaşi a scris:
Vă prezint mai jos o funcţie care leagă un număr prim p de ordinalul său n, mai precis, o funcţie care ne permite să calculăm al câtelea număr prim este p. Ea a fost dedusă în 1994 pe fişa mea cu numărul 610.

Aşadar, dat fiind un număr prim p>1 funcţia următoare ne calculează ordinalul acestui număr prim: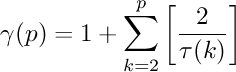

unde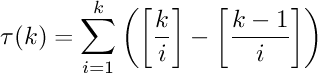

este numărul de divizori ai lui k, iar parantezele drepte semnifică funcţia „parte întreagă”.

Demonstraţia este simplă, fiind suficient să observăm că funcţia $Problema numerelor prime - Pagina 3 Mimetex$ se incrementează doar atunci când k este prim.

Problema fundamentală a numerelor prime ar putea fi rezolvată dacă am putea inversa această funcţie şi puteţi vedea pe aceeaşi fişă nişte încercări inocente în această direcţie, continuate pe fişa cu numărul 616.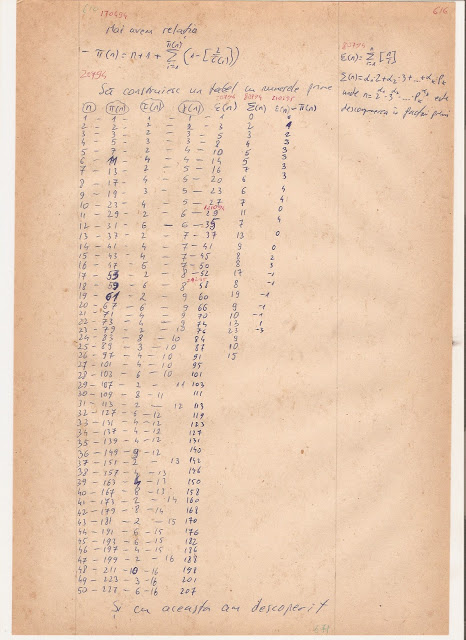

În schimb, pe fişa cu numărul 671 (în continuarea fişei 616) am emis chiar pretenţia că aş fi găsit o asemenea funcţie inversă.

Scris de **curiosul** Lun 10 Sept 2012, 14:43

Vad hartii cu numere !!!
Deja incep sa mi se invarta neuronii de parca au intrat intr-o gaura neagra.
Abel,
o sa analizez cu atentie hartiile tale,
inainte sa afirm ceva.
Ai ceva rabdare.

Scris de **curiosul** Lun 10 Sept 2012, 16:07

Pentru moment, functia pe care ai dedus-o in ultima fisa, este izbitor de aemanatoare cu cea pe care am dedus-o eu intr-unul din subiectele de pe acest forum :

$1-\left \{ \sum_{p_{1}}^{p_{n}}\left [ \frac{1}{p}\prod_{p_{1}}^{p_{n-1}}\left ( 1-\frac{1}{p} \right ) \right ] \right \}$

Diferenta apare prin faptul ca fiecare dintre noi s-a rezumat la alt "punct de reper" :
-tu te-ai legat de functia care calculeaza divizorii
-eu am tinut cont de numarul de numere prime care pot divide numarul n.

Cred ca pot "contura" ceva comun.
Revin.

Scris de **Dacu** Lun 10 Sept 2012, 20:40

Abel Cavaşi a scris:Aşa cum am promis la începutul acestui topic:
La începutul acestui topic, Abel Cavaşi a scris:Cândva, pe vremea când aveam mai mult timp liber, am găsit o soluţie la problema inversă: dându-se numărul prim p, să se găsească al câtelea număr prim este el în şirul numerelor prime. Dacă o voi găsi printre hârtiile mele vechi, o voi posta aici. Ştiu că era ceva cu partea întreagă a unui număr.
,
postez aici ceea ce am scris şi pe blogul meu prin 2011:

Pe blogul său, Abel Cavaşi a scris:
Vă prezint mai jos o funcţie care leagă un număr prim p de ordinalul său n, mai precis, o funcţie care ne permite să calculăm al câtelea număr prim este p. Ea a fost dedusă în 1994 pe fişa mea cu numărul 610.

Aşadar, dat fiind un număr prim p>1 funcţia următoare ne calculează ordinalul acestui număr prim: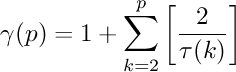

unde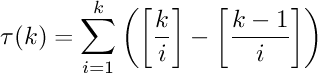

este numărul de divizori ai lui k, iar parantezele drepte semnifică funcţia „parte întreagă”.

Demonstraţia este simplă, fiind suficient să observăm că funcţia $Problema numerelor prime - Pagina 3 Mimetex$ se incrementează doar atunci când k este prim.

Problema fundamentală a numerelor prime ar putea fi rezolvată dacă am putea inversa această funcţie şi puteţi vedea pe aceeaşi fişă nişte încercări inocente în această direcţie, continuate pe fişa cu numărul 616.

În schimb, pe fişa cu numărul 671 (în continuarea fişei 616) am emis chiar pretenţia că aş fi găsit o asemenea funcţie inversă.

Daca se poate as dori sa vad cativa termeni ai sumei $Problema numerelor prime - Pagina 3 Mimetex$ .Multumesc!

Scris de **Dacu** Lun 10 Sept 2012, 20:42

curiosul a scris:Pentru moment, functia pe care ai dedus-o in ultima fisa, este izbitor de aemanatoare cu cea pe care am dedus-o eu intr-unul din subiectele de pe acest forum :

$1-\left \{ \sum_{p_{1}}^{p_{n}}\left [ \frac{1}{p}\prod_{p_{1}}^{p_{n-1}}\left ( 1-\frac{1}{p} \right ) \right ] \right \}$

Diferenta apare prin faptul ca fiecare dintre noi s-a rezumat la alt "punct de reper" :
-tu te-ai legat de functia care calculeaza divizorii
-eu am tinut cont de numarul de numere prime care pot divide numarul n.

Cred ca pot "contura" ceva comun.
Revin.

Fara suparare dar nu vad care e asemanarea cu $Problema numerelor prime - Pagina 3 Mimetex$ .

Scris de **curiosul** Lun 10 Sept 2012, 23:10

Atat timp cat vorbesti frumos, nu se supara nimeni Dacu(le).
Vezi ca am zis "ultima fisa".
Pe ultima fisa nu este "y(p)".
Uita-te la modul in care este dezvoltata seria din ultima fisa a lui Abel, si la modul in care se dezvolta seria la care fac eu referire.
Mai vorbim cand o sa vin cu comentariile concrete si complete.
Acum, inca analizez corectitudinea rationamentelor lui Abel.

Scris de **Abel Cavaşi** Lun 10 Sept 2012, 23:28

curiosul a scris:Pentru moment, functia pe care ai dedus-o in ultima fisa, este izbitor de aemanatoare cu cea pe care am dedus-o eu intr-unul din subiectele de pe acest forum :

$1-\left \{ \sum_{p_{1}}^{p_{n}}\left [ \frac{1}{p}\prod_{p_{1}}^{p_{n-1}}\left ( 1-\frac{1}{p} \right ) \right ] \right \}$

Ciudat, mie nu-mi par a fi asemănătoare. Dar mă bucur că munca mea ţi-a trezit interesul.

Dacu a scris:Daca se poate as dori sa vad cativa termeni ai sumei $Problema numerelor prime - Pagina 3 Mimetex$ .Multumesc!

Pe fişa 616 ai o mulţime de asemenea termeni.

Problema numerelor prime - Pagina 3 Fise%252520601-700-15

Alege-i pe aceia care îţi plac.

Scris de **Dacu** Mar 11 Sept 2012, 07:41

Fara suparare!Pe fisa aia nu vad clar termenii lui $Problema numerelor prime - Pagina 3 Mimetex$ .Inteleg ca $Problema numerelor prime - Pagina 3 Mimetex$ este un numar prim si ca acea suma este de la $Problema numerelor prime - Pagina 3 Mimetex$ la $Problema numerelor prime - Pagina 3 Mimetex$ si atunci intreb care sunt valorile lui $Problema numerelor prime - Pagina 3 Mimetex$ si anume $Problema numerelor prime - Pagina 3 Mimetex.cgi?{k=p_1,p_1+1,p_1+2,......$ unde $Problema numerelor prime - Pagina 3 Mimetex$ este un numar prim astfel incat $Problema numerelor prime - Pagina 3 Mimetex$ ?

Scris de **Dacu** Mar 11 Sept 2012, 08:20

Fara suparare!Referitor la $Problema numerelor prime - Pagina 3 Mimetex$ pentru $Problema numerelor prime - Pagina 3 Mimetex$ rezulta ca in cazul cand calculam direct (caci $Problema numerelor prime - Pagina 3 Mimetex$ reprezinta numarul divizorilor lui $Problema numerelor prime - Pagina 3 Mimetex$ ) atunci $Problema numerelor prime - Pagina 3 Mimetex$ deoarece 2 are patru divizori ori se stie ca numarul 2 este primul numar prim si chiar daca am elimina doi divizori ai lui 2 tot ar reiesi ca ordinalul lui 2 este 2 cand de fapt el trebuie sa fie 1.Totodata am nelamuriri la modul cum se calculeaza $Problema numerelor prime - Pagina 3 Mimetex$ si as dori sa vad care sunt termenii acestuia intrucat chiar nu inteleg cum se genereaza.As dori daca se poate sa fie date cateva exemple pentru calculul ordinalului a catorva numere prime sa zicem pentru 5,13 si 23 caci din acele fise nu vad si nici nu prea inteleg bine. Multumesc!

Scris de **Abel Cavaşi** Mar 11 Sept 2012, 08:28

[Offtopic]
Dacu(le), dar de ce aş avea motive să mă supăr? Mă crezi chiar aşa supărăcios? Sau crezi că m-ai jignit în cine ştie ce hal pentru că nu eşti de acord cu anumite lucruri pe care le spun? Fii liniştit, omule, contrazi-mă ori de câte ori simţi nevoia sinceră să faci asta!
[/Offtopic]

Funcţia $Problema numerelor prime - Pagina 3 Mimetex$ este ordinalul unui număr prim. Adică ne arată al câtelea număr prim este numărul p. O găseşti pe coloana din mijloc (a patra) pe fişă. Şi nu uita, ne limităm la valorile naturale ale numerelor prime şi, implicit, ale divizorilor.

Scris de **curiosul** Mar 11 Sept 2012, 09:45

Abel, Dacu,
hai sa vedem pentru inceput daca ma insel sau nu,
sau si eu, la randul meu, ma grabesc sa afirm lucruri insuficient anailizate.
In functie de raspunsurile voastre, cred ca putem ajunge la a "contura" ceva comun.
Nu vreau sa incarc acest mesaj cu multe dezvoltari care ar ingreuna intelegerea lor, si propun sa le luam la rand.
Deci,

sunteti de acord ca modul in care este definita seria :

$\tau(k)=\sum_{i=1}^{k}\left ( \left [ \frac{k}{i} \right ]-\left [ \frac{k-1}{i}\right ] \right )\simeq \sum_{i=1}^{k}\left ( \left [ \frac{k}{i}-\frac{k-1}{i} \right ] \right )$

si s-ar reduce la faptul ca :

$\tau(k)=\sum_{i=1}^{k}\left [ \frac{1}{i} \right ]$

unde parantezele patrate semnifica acelasi lucru pe care l-a subliniat Abel.
Voi continua in functie de raspunsul vostru.

Scris de **Abel Cavaşi** Mar 11 Sept 2012, 09:55

Eu nu pot fi de acord cu această aproximaţie. Pentru că numărul de divizori este foarte divers, spre deosebire de ultima sumă care este invariabil egală cu unitatea.

Scris de **curiosul** Mar 11 Sept 2012, 10:21

Da Abel, ai dreptate,
analizand ultima expresie in functie de partea intreaga, ea se reduce la a fi egala cu unitatea.
Cred ca mai degraba as fi vrut sa spun:

$\tau (k)=\sum_{i=1}^{k}\frac{1}{i}$

Scris de **Abel Cavaşi** Mar 11 Sept 2012, 10:28

Chiar şi aşa, numărul de divizori ai unui număr natural este extrem de diferit de suma armonică cu care ai vrea să-l aproximezi. Eu nu pot accepta această aproximaţie şi-ţi recomand s-o „uiţi”, ca să te poţi concentra cu adevărat la lucruri (ce mie mi se par a fi) mai interesante.

Scris de **curiosul** Mar 11 Sept 2012, 10:29

Scuze, rectific :

$\tau (x)=\left [ \sum_{i=1}^{k}\frac{1}{i} \right ]$

Mi-as dori daca se poate modifica cu inca vreo 5 min, timpul de editare al mesajului.

Scris de **curiosul** Mar 11 Sept 2012, 10:31

Ok.
Referitor la ultimul tau mesaj.

Scris de **Abel Cavaşi** Mar 11 Sept 2012, 10:40

curiosul a scris:Scuze, rectific :

$\tau (x)=\left [ \sum_{i=1}^{k}\frac{1}{i} \right ]$

Nici aşa nu-mi place. Numărul de divizori nu este o funcţie monotonă, pe când suma propusă de tine este.

[Offtopic]

Mi-as dori daca se poate modifica cu inca vreo 5 min, timpul de editare al mesajului.

S-a rezolvat. Am mărit la 10 minute timpul de editare.
[/Offtopic]

Scris de **curiosul** Mar 11 Sept 2012, 11:08

Abel nu vreau sa crezi ca te contrazic doar pentru ca nu esti de acord cu mine. Din contra, vreau sa ajungem la o concluzie pe care sa o acceptam amandoi.

Daca am dezvoltat-o corect, functia :

$\sum_{i=1}^{k}\left ( \left [\frac{k}{i} \right ]-\left [ \frac{k-1}{i} \right ] \right )$

este si ea monotona pe anumite intervale, cum este si :

$\left [ \sum_{i=1}^{k}\frac{1}{i} \right ]$

Suntem de acord amandoi ca numarul divizorilor nu poate fi descrisa de o functie monotona.

Insa daca functia : $\sum_{i=1}^{k}\left ( \left [\frac{k}{i} \right ]-\left [ \frac{k-1}{i} \right ] \right )$ este monotona pe anumite intervale, ma gandesc ca nici functia :

$\gamma(p)=1+\sum_{k=2}^{p}\left [ \frac{2}{\tau (k)} \right ]$ nu "descrie" corect relatia $P_{n}\overset{\gamma (p)}{\rightarrow}n$
in functie de $\tau (p)$ .
Aproximarile din tabelul tau, sunt exemplificatoare doar pentru partea de inceput a sirului numerelor prime.

Insa, pentru faptul ca la nivelul unor valori foarte mari,functia $\tau (p)$ descrie din ce in ce mai incorect numarul divizorilor unui numar, aproximarea prin functia $\gamma (p)$ a relatiei $P_{n}\overset{\gamma (p)}{\rightarrow}n$ este la randul ei din ce in ce mai diferita fata de valoarea reala.

Cu siguranta, imi dau seama ca la fel se comporta si $\left [ \sum_{i=1}^{k}\frac{1}{i} \right ]$ .

Sper sa nu ma intelegi gresit.
vad totusi, in seria de pe ultima fisa, ceva interesant, dar care presupune din punctul meu de vedere, corectarea functiei, daca este cazul si nu ma insel eu, $\gamma (p)$

Oricum, incepe sa ma intereseze din ce in ce mai mult, o functie care ar descrie cu cat mai mare exactitate, divizorii unui numar.
Cu mare placere primesc "criticile" si corectarile tale.

Scris de **Abel Cavaşi** Mar 11 Sept 2012, 11:23

curiosul a scris:Aproximarile din tabelul tau, sunt exemplificatoare doar pentru partea de inceput a sirului numerelor prime.

Nu văd care sunt aproximările de care vorbeşti. Eu n-am aproximat nimic acolo. Totul este calculat cu precizie completă. Şi ceea ce am scris nu este valabil doar pentru primele numere, ci pentru toate.

Oricum, incepe sa ma intereseze din ce in ce mai mult, o functie care ar descrie cu cat mai mare exactitate, divizorii unui numar.

Dacă te interesează o asemenea funcţie, o ai deja acolo.

Scris de **curiosul** Mar 11 Sept 2012, 14:17

Ok, Abel.
Problema mea este ca eu caut exactitatea si nu aproximarile fata de valorile reale.
Calculele tale sunt exacte doar in ceea ce privesc valorile returnate de aceste functii , nu in ceea ce priveste valoarea data de functie fata de valoarea reala .

Dar ma gandesc ca tu stii mai bine ce spui.

Scris de **Abel Cavaşi** Mar 11 Sept 2012, 17:15

Înţeleg că te nemulţumeşte ciudăţenia funcţiei parte-întreagă de a „arunca” la gunoi atâtea zecimale valoroase din care s-ar putea extrage atâta informaţie valoroasă necesară pentru inversarea funcţiei. Asta e, matematica ştie să lucreze şi cu asemenea concepte, oricât ar fi ele de „respingătoare”.

Scris de **totedati** Mier 12 Sept 2012, 11:46

mie de exemplu mi se pare interesant faptul că diferența dintre două numere prime e număr par la fel ca suma a două numere prime și că e relativ ușor de demonstrat asta ...

iar valoarea diferenței pare la fel de imprevizibilă ca și șirul numerelor prime!

LE: de fapt e chiar mai ciudat! după un mic test în excel văd că paritatea diferenței sau sumei e valabilă pentru oricare două numere prime aflate la n apariții consecutive una de cealaltă! în afară de capul seriei, totdeauna impar, restul șirului e par!

ceea ce ne arată că șirul numerelor prime 2,3,5,7 ... n conține un subșir distinct de numere 3,5,7 ... n care par a fi în aceeași relație cu numărul 3, capul seriei, ca șirul nr. prime față de capul seriei, numărul prim 2!

suma a două numere pare consecutive e tot timpul mai mare ca următorul număr prim

suma a trei numere pare consecutive din care scădem următorul număr prim e număr par dacă excludem din serie capul seriei, primele 4 numere prime consecutive

am descoperit și șirul divizibil cu 3:

p1+p2-p3=0
p1+p2+p3-p4=3
p1+p2+p3+p4-p5=6
p1+p2+p3+p4+p5-p6=15
p1+p2+p3+p4+p5+p6-p7=24

3, 6, 15, 24, 39, 54 ....

parcă e divizibil cu 3 șirul! suma a n numere prime minus următorul număr prim e divizibil cu trei dacă și numai dacă suma a n-1 numere prime din care scădem următorul număr prim e divizibil cu trei!

lol! foarte ciudat saltul de la capul de serie 2 la capul de serie 3!

Scris de **curiosul** Mier 12 Sept 2012, 13:04

totedati,

poti sa fi un pic mai explicit in ceea ce priveste :

"LE: de fapt e chiar mai ciudat! după un mic test în excel văd că paritatea diferenței sau sumei e valabilă pentru oricare două numere prime aflate la n apariții consecutive una de cealaltă! în afară de capul seriei, totdeauna impar, restul șirului e par!

ceea ce ne arată că șirul numerelor prime 2,3,5,7 ... n conține un subșir distinct de numere 3,5,7 ... n care par a fi în aceeași relație cu numărul 3, capul seriei, ca șirul nr. prime față de capul seriei, numărul prim 2!"

Scris de **totedati** Mier 12 Sept 2012, 13:24

adică e valabil și pentru șirul

p2-p1=1
p3-p2=2
p4-p3=2
.
4, 2, 2 ....

și pentru șirul

p10-p1=27
p11-p2=28
p12-p3=32
.
34, 32, 34, 36 ...

șamd .... totdeauna capul de serie impar și restul numere pare indiferent cît de mult sari în șirul de numere prime ...

LE:
conjectură empirică:

șirul de numere

p2-p1
p3-p1
p4-p1
.
pn-p1

e următorul cel mai dens șir în numere prime după șirul numerelor prime care evident are densitatea maximă ....

1, 3, 5, 9, 11, 15, 17, 21, 27, 29, 35, 39, 41, 45, 51, 57, 59, 65, 69, 71, 77, 81, 87, 95, 99, 101 șamd ...

λ(1)=0
λ(2)=1 vs. P(2)=2
λ(3)=2 vs. P(3)=3
λ(4)=2
λ(5)=3 vs. P(5)=5
λ(6)=3
λ(7)=4 vs. P(7)=7
λ( Cool

=4

șamd ....

pare destul de dens în numere prime ... are cineva un șir mai dens?

următorul cel mai dens șir în numere prime e evident
p(3)-p(2)
p(4)-p(2)
p(5)-p(2)
p(6)-p(2)
.
.
p(n)-p(2)
șamd ....

Scris de **curiosul** Mier 12 Sept 2012, 13:41

Ok.
Am inteles ce vrei sa spui.
O sa-ti explic si de ce ti "se pare" ca este asa.
Dar mai intai, mai calculeaza un pic si pentru numere mai mari sa vezi daca aceasta "constanta" se mai respecta.
Vei vedea ca nu.

Scris de **totedati** Mier 12 Sept 2012, 14:11

ai cunoștință de ceva contra-exemple?

pune dovezile pe masă!

cînd am timp o să lungesc șirurile pînă la 10k numere prime să văd dacă mai sunt respectate empiric ... deocamdată mă lupt cu openoffice să văd cum pot colora doar numerele prime dintr-un astfel de șir cînd plec de la un tabel deja calculat de numere prime ...

dacă e corect ce mi se pare mie ar trebui să poată fi și demonstrat la fel de ușor ca în cazul cel mai simplu, suma sau diferența a două numere prime consecutive unde deja sa demonstrat ...

n-are cum să le fi descoperit doar eu acum!

pentru p₍ₙ₊₁₎ - pₙ e simplu:

din pₙ > 2 și prim avem pₙ număr impar deci pₙ-1=2A
la fel p₍ₙ₊₁₎ > 2 și prim avem p₍ₙ₊₁₎ -1 =2B

2B-2A=2(B-A)
2(B-A) +1 +1 = 2(B-A)+2=2(B-A+1)

B-A>1 ∀n>2 deci șirul e pozitiv și crescător și demonstrabil par pentru n oricît de mare dacă scoatem capul de serie, p(1)=2, din șir ...

însă se pare că mai sunt o grămadă de alte șiruri generate din șirul numerelor prime la fel de interesante!

Scris de **curiosul** Mier 12 Sept 2012, 14:22

Deci,
totedati,
numerele prime sunt 2,3,5,7,11,13,..etc.

Sa incepem cu primul.
Hai sa aranjam toate numerele in linii de P(1), adica 2 :

1.3.5.7.9,...
2,4,6,8,....

Se observa ca numerele care nu se divid cu 2, adica numerele impare, se gasesc pe aceeasi linie, adica intr-o constanta de 2.
Ok.
Acum hai sa aranjam toate numerele naturale P(1)*P(2) linii, adica in 6=2*3 linii :
1, 7. 13,..
2, 8, 14,..
3, 9, 15,..
4,10, 16,..
5,11, 17,..
6, 12,18,..

Observi cu usurinta ca numerele care se divid cu P(1) si cu P(2), sau si cu P(1) si P(2), adica P(1)*P(2) se gasesc pe aceleasi linii.
Asta determina o constanta de aparitie a lor, adica a numerelor care nu se divid nici cu P(1) nici cu P(2) [consideri numarul 1 inclus in aceasta constanta] :
1, 5, 7, 11, 13, 17, 19, 23, 25, 29,...
Se observa ca ele se gasesc distribuite dupa constanta:
4, 2, 4, 2, 4, 2, 4, 2....

Continuam rationamentul.
Daca luam in calcul numerele care nu se divid cu numerele prime 2, 3 si 5, vom observa ca toate numerele care nu se divid cu 2, 3 si 5, se gasesc distribuite in numere dupa constanta:
6, 4, 2, 4, 2, 4, 6, 2.
Vei observa ca aceasta constanta, adica suma numerelor care reprezinta distanta dintre numerele care nu se divid cu 2,3 si 5, este egala cu 30.
Surpriza !
Adica exact 2*3*5 !

Deci se pare ca toate numerele care nu se divid cu 2, 3, 5, 7, ..., P(n) se gasesc in numere cu o periodicitate de 2*3*5*7*...*P(n).
Deci se pare ca exista o constanta diferita in acest sens, caracteristica oricarui numar prim.
Dar 1 trebuie luat in calcul.

Constanta pe care ai gasit-o tu si care ti se pare interesanta se datoreaza efectiv acestei reguli.
Capisci ?

Insa, fie ca vrei sa ma crezi sau nu, raportat la sirul total al numerelor prime, NU EXISTA O CONSTANTA !
Poti sa faci calcule pana la adanci batraneti.
cand voi termina lucrarea despre numerele prime, acolo vei gasi si o demonstratie completa a faptului ca nu exista o asemenea constanta.

Rationamentul pe care ti l-am dezvoltat mai sus, este singurul tip de constanta care poate fi construit raportat la numerele prime.
Insa el este suficient pentru a demonstra ca in numere, densitatea numerelor prime este determinata doar de aceasta constanta.
Deja intram pe un teritoriu pe care nu ti-l mai pot explica usor.
Dar toate la timpul lor.
Cu stima totedati, este un subiect pe care il stapanesc mai bine ca tine, din cate am observat.
Eu iti raspund la nedumeririle tale atat timp cat imi dai de inteles ca vrei sa intelegi ce spun, in niciun caz daca tii mortis sa-mi dovedesti ca ai dreptate.
Cu lipsa de modestie afirm asta, pentru ca stiu ce stiu.
Cu prietenie totedati.

Scris de **totedati** Mier 12 Sept 2012, 14:44

nici o problemă eu abordez subiectul după ureche, adică băbește, cum suntem în sec. XXI upgradat de la creion și hîrtie la libre office calc și tabele de numere prime deja calculate pînă la generația XXL ...

deocamdată parcă sunt niște reguli ... evident empirice ... din ce susții tu înțeleg că șirul numerelor prime e atît de ciudat încît fără o demostrație matematică clară putem avea șiruri cu milioane de termeni calculați empiric care să se potrivească boboc, cum ar fi exemplul meu cu șirul divizibil la 3, tot nu putem fi siguri că e o teorie matematică în spatele șirului de numere care își așteaptă demonstrația sau doar o iluzie optică!

pînă nu demonstrăm la fel de simplu ca la p₍ₙ₊₁₎ - pₙ=2Z nici un șir de combinații de numere prime calculate empiric, oricît de lung și indiferent de regulile de generare nu e suficient de lung!

Scris de Continut sponsorizat

Problema numerelor prime

Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime

Re: Problema numerelor prime